Questões sobre Probabilidade

O tempo de funcionamento até a ocorrência de falha em uma velha máquina é uma variável aleatória exponencial com média igual a 10 dias. O proprietário da máquina decide colocar a máquina em funcionamento por 30 dias. Considere que o número de falhas segue um processo de Poisson homogêneo. Com base nessas informações, julgue os itens que se seguem.

Dado que a máquina funcionou sem falhar nos primeiros 10 dias, a probabilidade de ela não falhar nos 20 dias seguintes é igual a exp(-2), em que exp(.) representa a função exponencial.

• C. Certo
• E. Errado

• C. Certo
• E. Errado

Para resolver as questões de números 31 a 33, utilize, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

P (Z > 2) = 0,023, P (Z < 1,64) = 0,945,

P (0 < Z < 1,5) = 0,433, P (Z < 1,34) = 0,91

Uma corretora de ações, que opera numa certa Bolsa de Valores, faz aplicações financeiras de compra e venda de ações nas áreas Industrial e Comercial, e faz uso de um modelo de probabilidades para a avaliação de seus lucros. O modelo que representa o lucro diário da corretora (em milhares de reais) é dado por:

L = 2 L_I + 3 L_C,

onde

L_I = lucro diário da área Industrial tem distribuição normal com média 5 e variância 16,

L_C = lucro diário da área Comercial tem distribuição normal com média 4 e variância 4.

Supondo independência entre as duas variáveis que compõem L, a probabilidade de um lucro diário superior a 37 mil é

• A. 6,7%
• B. 7,3%
• C. 8,1%
• D. 9,5%
• E. 12,4%

A temperatura T de destilação do petróleo é uma variável aleatória com distribuição uniforme no intervalo [150, 300]. Seja C o custo para se produzir um galão de petróleo. Determine o lucro esperado por galão, supondo que o preço de venda por galão é uma variável aleatória Y dada por: 

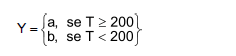
• A. (a + 2b) / 3 − C
• B. (a − C) / 150 + (b − C) / 50
• C. (a + b) / 3 − C
• D. (a + b) / 150 − C
• E. (2a + b) / 3 − C

Seja X uma variável aleatória com função densidade de probabilidade dada por:

• A. e^–4
• B. e^–2
• C. e^–1
• D. e^–1/2
• E. 1

Na transmissão de informação digital, a probabilidade de um bit recebido é classificado como aceitável, suspeito ou inaceitável, dependendo da qualidade do sinal recebido, com probabilidades iguais a 0,8; 0,10 e 0,10, respectivamente. Suponha que as classificações de cada bit sejam independentes. Nos quatro primeiros bits recebidos, seja X o número de bits aceitáveis e Y o número de bits suspeitos. Então P (X = 2, Y = 1) é dada por

• A. 0,00256
• B. 0,00384
• C. 0,00512
• D. 0,0064
• E. 0,0768

Sabe-se que a variável aleatória X é bi-modal para x = 1 e x = 2 e que tem distribuição de Poisson. Sabendo que X é diferente de zero, a probabilidade de X assumir um valor menor do que 3 é dada por

• A.
• B.
• C.
• D.
• E.

Sejam A e B dois eventos associados a um experimento. Supondo que P(A) = 0,4 e P(AUB) = 0,7 e P(B) = p. Os valores de p que fazem com que A e B sejam mutuamente exclusivos e A e B sejam independentes são, respectivamente,

• A. 0,3 e 0,5
• B. 0,4 e 0,2
• C. 0,5 e 0,2
• D. 0,6 e 0,2
• E. 0,3 e 0,4

As informações a seguir referem-se às questões de números 54 e 55.

Seja a variável aleatória bidimensional (X, Y), com função densidade de probabilidade conjunta dada por

f(x, y) = x + y, 0 < x < 1, 0 < y < 1

• A. 1/6
• B. 1/8
• C. 1/10
• D. 1/12
• E. 1/16

Uma rede local de computadores é composta por um servidor e 2 (dois) clientes (Z e Y). Registros anteriores indicam que dos pedidos de certo tipo de processamento, cerca de 30% vêm de Z e 70% de Y. Se o pedido não for feito de forma adequada, o processamento apresentará erro. Sabendo-se que 2% dos pedidos feitos por Z e 1% dos feitos por Y apresentam erro, a probabilidade do sistema apresentar erro é

• A.

  5%

• B.

  4,1%

• C.

  3,5%

• D.

  3%

• E.

  1,3%