Questões sobre Probabilidade

Com a seguinte função de probabilidade conjunta, onde x assume os valores 0 e 1, e y assume os valores, 1, 2 e 3,

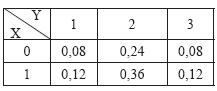
pode-se afirmar que

• A.

  P(Y = 3) = 0,08.

• B.

  P(X =0) = P(Y =2).

• C.

  P(Y = 2 / X = 0) = 0,6.

• D.

  E(X) = 0,4.

• E.

  X e Y são variáveis aleatórias dependentes.

Dois novos tipos de vacina contra determinada doença estão sendo testados: a vacina do tipo A e a vacina do tipo B. Esses dois tipos de vacinas foram aplicados em uma população de voluntários. Sabe-se que 60 % dos voluntários receberam vacina do tipo A e 40% dos voluntários restantes receberam vacina do tipo B. Sabe-se, também, que a vacina do tipo A fornece 70% de imunização e a do tipo B fornece 80% de imunização. Assim, a probabilidade de uma pessoa, escolhida ao acaso, estar imunizada dado que lhe foi aplicada a vacina do tipo A é igual a

• A.

  0,5.

• B.

  0,42.

• C.

  0,68.

• D.

  21/37.

• E.

  42/75.

O Teorema de Bayes diz que, para dois eventos independentes, A e B, com probabilidades não nulas, tem-se que

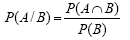
onde, P(A/B) é a probabilidade de ocorrer o evento A, sabendo-se que o evento B já ocorreu. Desse modo pode-se afirmar que

• A.

  se A e B são eventos mutuamente excludentes, então P(A/B) = P(A).

• B.

  se P(B/A) = P(B), então A e B são eventos dependentes.

• C.

  se P(A) ≠ P(B), então A e B são eventos independentes.

• D.

  se P(A) ≠ P(B), então A e B são eventos dependentes.

• E.

  se P(A ∩ B) = 0, então A e B são eventos independentes.

Uma variável aleatória contínua, x, tem função densidade de probabilidade igual a: f(x) = 2x, para 0 < x < 1 e f(x) = 0 para qualquer outro valor de x que estiver fora deste intervalo. Assim, pode-se afirmar que

• A.

  P (0< x < 0,2) = 0,2

• B.

  P (0< x < 0,2) = 0,4

• C.

  P (0< x < 0,2) = 0,24

• D.

  P (0< x < 0,2) = 0,06

• E.

  P (0< x < 0,2) = 0,04

Para a Gincana Cultural organizada pelos Professores do Cefet, foi escolhido os grupos de alunos, da seguinte forma:

Escolhendo-se um aluno aleatoriamente, qual a probabilidade do aluno sorteado ser um homem, sobendo-se que a disciplina sorteada foi Inglês?

• A. 1/47
• B. 47/360
• C. 47/99
• D. 47/52
• E. 1/360

A "Lei dos Grandes Números" estabelece que à medida que aumenta o número de vezes, n, que se repete um experimento probabilístico, tem-se que

• A.

  a probabilidade teórica da ocorrência de um evento tende para sua freqüência absoluta, se n > 10.

• B.

  a freqüência absoluta de um evento tende para a sua probabilidade teórica, se n > 30.

• C.

  a freqüência relativa de um evento tende para o desvio relativo do evento, se n > 100.

• D.

  freqüência relativa de um evento tende para sua probabilidade teórica, se n for suficientemente grande.

• E.

  a freqüência relativa de um evento tende para sua probabilidade teórica, independente de n.

Uma rede local de computadores é composta por um servidor e 2 clientes (A e B). Registros anteriores indicam que, dos pedidos de certo tipo de processamento, cerca de 30% vêm de A e 70% de B. Se o pedido não for feito de forma adequada, o processamento apresentará erro. Sabe-se que 2% dos pedidos feitos por A e 5% dos feitos por B apresentam erro. Selecionando um pedido ao acaso, a probabilidade dele ser proveniente de A, sabendo que apresentou erro, é

• A.
• B.
• C.
• D.
• E.

Considere, no plano cartesiano, o quadrado com vértices (0,0), (0,2), (2,0), (2,2). Suponha que a probabilidade da região A (evento) seja a área dessa região dividida por quatro. A probabilidade do evento 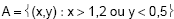 é

• A. 0,15
• B. 0,30
• C. 0,40
• D. 0,50
• E. 0,55

Instruções: Para responder às questões de números 34 e 35 considere a informação abaixo.

O número de falhas de certo tipo de placa térmica tem distribuição de Poisson, com taxa média de 0,1 defeitos por m2. Na confecção da superfície de um armário, é necessário cobrir uma superfície de 2 m × 2 m com essa placa.

A probabilidade de que haja pelo menos uma falha nessa superfície é

• A. e^−0,1
• B. 1 − e^−0,1
• C. 1 − e^−0,4
• D. e^−0,4
• E. 1 − 1,4e^−0,4

Instruções: Para responder às questões de números 34 e 35 considere a informação abaixo.

O número de falhas de certo tipo de placa térmica tem distribuição de Poisson, com taxa média de 0,1 defeitos por m2. Na confecção da superfície de um armário, é necessário cobrir uma superfície de 2 m × 2 m com essa placa.

Na confecção de 3 superfícies deste tipo, a probabilidade de que exatamente duas não apresentem defeito é

• A. 3(1− e^−0,4 )² e^−0,4
• B. 3 e^−0,1
• C. 3(1− e−^0,2 )
• D. 3(1− e^−0,1 )² e^−0,1
• E. 3(1− e^−0,4 ) e^−0,8