Questões sobre Probabilidade

Instruções: Para responder às questões de números 55 e 56 utilize, dentre as informações abaixo, as que julgar adequadas. Se Ζ tem distribuição normal padrão, então:

 P(0< Ζ < 1) = 0,341 , P(0< Ζ < 1,6) = 0,445 , P(0< Ζ < 2) = 0,477

Os depósitos efetuados no Banco B, num determinado mês, têm distribuição normal com média R$ 9.000,00 e desvio padrão R$ 1.500,00. Um depósito é selecionado ao acaso dentre todos os referentes ao mês em questão. A probabilidade de que o depósito exceda R$ 6.000,00 é de

• A. 97,7%
• B. 94,5%
• C. 68,2%
• D. 47,7%
• E. 34,1%

Os eventos E₁ e E₂ são os conjuntos de pontos que podem estar tanto em E₁ quanto em E₂, como em ambos, simultaneamente. Então, a probabilidade de uma ocorrência ser do evento E₁ ou E₂ é dada por:

• A. (E₁ + E₂) = P(E₁) + P(E₂).
• B. P (E₁ + E₂) = P(E₁) + P(E₂) - P (E₁ E₂).
• C. P (E₁ + E₂) = P(E₁) + (1 - P(E₂).
• D. P (E₁ + E₂) = P(E₂) + (1 - P(E₁)).
• E. P (E₁ + E₂) = P(E₁) * P(E₂).

Um grupo de 1.000 pessoas tem a seguinte composição etária (em anos):

 - [ 0 - 20]: 200 pessoas;

 - [21 - 30]: 200 pessoas;

- [31 - 40]: 200 pessoas;

 - [41 - 50]: 200 pessoas;

 - de 51 anos em diante: 200 pessoas.

Considerando que as probabilidades média de morte (qx), segundo uma determinada tábua, é de:

 - [0 - 20] até 20 anos: 0,600% o (por mil);

- [21 - 30]: 0,800%o (por mil);

 - [31 - 40]: 1,500%o (por mil);

 - [41 - 50]: 5,000%o (por mil);

- de 51 anos em diante: 20,000% o (por mil).

 Pode-se afirmar que a possibilidade de ocorrer a morte de exatamente 10 pessoas com idade superior a 51 anos é um evento:

• A. Certo.
• B. Impossível.
• C. Provável.
• D. Muito Provável.
• E. Pouco Provável.

Se p é a probabilidade de um evento acontecer em uma tentativa única e seu complemento (1 – p) é a probabilidade do evento não ocorrer (distribuição binomial), então a probabilidade do evento ocorrer exatamente X vezes, em n tentativas é dada por:

• A. p(X) = _nC_X p^X q^n-X
• B. p(X) = 1 - p^X q^n-X
• C. p(X) = p^X q^n-X
• D. p(X) = 1 + _nC_X p^X q^n-X
• E. p(X) = p^X - q^n-X

Se a variável X pode assumir um conjunto infinito (contínuo) de valores, o polígono de freqüência relativa de uma amostra torna-se uma curva contínua, cuja equação é Y = p(X). A área total limitada por essa curva e pelo eixo dos X é igual a 1 e a área compreendida entre as verticais X = a e X = b, sendo a < b e, ambos, contidos na área total da curva, a probabilidade de X cair neste intervalo a e b é dada por:

• A.

  <X

• B.
• C. P (a>X>b), composta pela soma de P(X=a) – P(X=b).
• D. P (a>X>b), composta pela integral de P(X=a) até P(X=b).
• E.

Seja X₁, X₂, ... uma sucessão de variáveis aleatórias identicamente distribuídas, cada uma com média 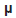 e variância ¶², tendo a propriedade de que qualquer número finito delas são independentes. Então, para cada z

onde Þ(z) é uma função de distribuição:

• A. Normal reduzida.
• B. Normal.
• C. Qui-quadrado.
• D. Log-normal.
• E. Binomial.

Para a resolução das questões que se seguem, lembre-se de que 90% da área abaixo da curva normal padrão se encontram entre -1,645 e 1,645, e 95% da área abaixo da curva normal padrão se encontram entre -1,96 e 1,96.

Uma moeda não-tendenciosa é lançada até que ocorram dois resultados sucessivos iguais. A probabilidade de que ela seja lançada quatro vezes é:

• A. 1/8.
• B. 3/8.
• C. 1/2.
• D. 5/8.
• E. 2/3.

Um grupo de 4 brasileiros e 4 bolivianos será aleatoriamente dividido em dois grupos de tamanho 4. A probabilidade de que ambos tenham o mesmo número de brasileiros e bolivianos é:

• A. 17/35;
• B. 1/2;
• C. 18/35;
• D. 19/35;
• E. 2/3.

Um equipamento de teste de falhas satisfaz a condição  com A={equipamento indica que componente é defeituoso}, é o complementar de A, B={o componente é defeituoso} e  é o complementar de B. A expectativa de um cliente é usar esse aparelho para localizar os componentes defeituosos em um grande lote de componentes no qual 10% são defeituosos. O valor de é:

• A. 1/10;
• B. 4/13;
• C. 1/2;
• D. 9/13;
• E. 9/10.

Para determinar se 60 pessoas em um grupo são portadoras ou não de certa doença, é necessário realizar um exame de sangue muito caro. Para contornar essa dificuldade, em vez de realizar 60 exames, decide-se distribuir essas pessoas em 4 grupos de 15 e juntar as amostras de sangue das pessoas de cada grupo, realizando-se inicialmente 4 exames, um para cada grupo. Em cada grupo, o sangue das quinze pessoas é coletado e misturado, e um único exame é realizado para essa amostra combinada. Se o exame da amostra combinada resulta negativo, conclui-se que nenhuma pessoa do grupo é portadora da doença e, assim, apenas um exame será realizado para esse grupo. Mas se o exame resulta positivo, conclui-se que pelo menos uma pessoa do grupo é portadora da doença e será necessário realizar um exame individual para cada membro desse grupo, de modo que serão realizados 16 exames para esse grupo. Se a probabilidade de ser portador da doença é 0,01 para todas as pessoas independentemente, o número esperado de exames em cada grupo é:

• A. 16(0,99)¹⁵ -15 ;
• B. 15(0,99)¹⁵ -1;
• C.

  16 -15(0,99)¹⁵ ;

• D. 15(0,99)¹⁵ +1;
• E.

  16 +15(0,99)¹⁵ .