Questões sobre Regressão

Com base nos resultados acima, conclui-se que

• A.

  a reta estimada é ˆ Y = 2,136 + 29,343x₁+ 4,477x₂.

• B.

  os coeficientes estimados são significativos ao nível de 1%.

• C.

  

• D.

  

• E.

  

Considere a tabela ANOVA (incompleta) a seguir.

Os valores de P, Q, R, S, T e U são, respectivamente,

• A.
• B.

  

• C.

  

• D.

  

• E.

  

Em um estudo sobre os preços médios pagos em aluguel de certa capital, foi utilizado o seguinte modelo:

O preço médio estimado de um imóvel com 3 quartos e área de 75 m² por esse modelo é de

• A.

  R$ 540,00.

• B.

  R$ 875,00.

• C.

  R$ 1.140,00.

• D.

  R$ 1.245,00.

• E.

  R$ 1.260,00.

Os quatro principais pressupostos da regressão são os seguintes:

• A.

  normalidade, homocedasticidade, independência de erros e linearidade

• B.

  normalidade, heterocedasticidade, independência de erros e linearidade

• C.

  normalidade, heterocedasticidade, dependência de erros e nã linearidade

• D.

  não normalidade, homocedasticidade, dependência de erros e não linearidade

• E.

  não normalidade, homocedasticidade, dependência de erros e não linearidade

O modelo de regressão múltipla é mais adequado para se obter o relacionamento entre os variáveis, peso, altura e sexo é:

• A.

  peso com idade e altura com sexo

• B.

  altura com idade e sexo com peso

• C.

  idade e sexo com altura e peso

• D.

  sexo com altura, idade e peso

• E.

  altura com a idade, peso e sexo

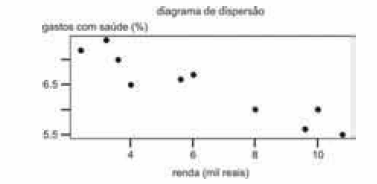
A figura acima corresponde a um diagrama de dispersão entre a variável y (gasto percentual com saúde) e x (renda bruta familiar, em R$ mil), obtida com base em uma amostra de 10 famílias. Com respeito ao ajuste de um modelo de regressão linear simples na forma y = ax + b + g, em que g é o erro aleatório e a e b são os coeficientes do modelo, foram obtidos os seguintes resultados.

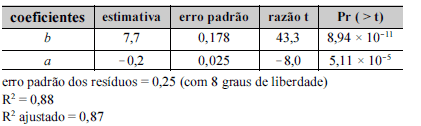
Com base nessas informações, julgue os itens seguintes.

Considerando que 1 < x < 10, é correto inferir que, a cada mil reais adicionais na renda bruta familiar, o gasto com saúde é reduzido em R$ 200,00.

• C. Certo
• E. Errado

Uma empresa de seguros deseja estimar z = preço esperado (em reais) de determinado tipo de motocicleta em função de x = tempo de uso (em anos) e de y = quilometragem rodada (em km). Para isso, a empresa levantou os dados de seis motocicletas, cujos valores estão na tabela a seguir.

Com relação ao modelo (1), a estimativa de mínimos quadrados do coeficiente a satisfaz à relação seguinte.

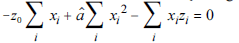
• C. Certo
• E. Errado

Uma empresa de seguros deseja estimar z = preço esperado (em reais) de determinado tipo de motocicleta em função de x = tempo de uso (em anos) e de y = quilometragem rodada (em km). Para isso, a empresa levantou os dados de seis motocicletas, cujos valores estão na tabela a seguir.

Com respeito ao modelo (1), o maior resíduo observado foi igual a R$ 1.500,00.

• C. Certo
• E. Errado

Uma empresa de seguros deseja estimar z = preço esperado (em reais) de determinado tipo de motocicleta em função de x = tempo de uso (em anos) e de y = quilometragem rodada (em km). Para isso, a empresa levantou os dados de seis motocicletas, cujos valores estão na tabela a seguir.

Considere que o modelo (2) seja adequado para descrever a relação entre x, y e z. Nessa situação, se uma moto, com um ano de uso, rodou 60.000 km e custa R$ 44.000,00 e se uma outra moto, com dois anos de uso, rodou 12.000 km e custa R$ 39.000,00, então, com base apenas nesses valores, é correto afirmar que a =12.000 e b = 0,1.

• C. Certo
• E. Errado

Uma empresa de seguros deseja estimar z = preço esperado (em reais) de determinado tipo de motocicleta em função de x = tempo de uso (em anos) e de y = quilometragem rodada (em km). Para isso, a empresa levantou os dados de seis motocicletas, cujos valores estão na tabela a seguir.

Considerando os dados da tabela, o modelo (1) fornece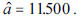

• C. Certo
• E. Errado