Questões sobre Teste de Hipótese

Em problemas de teste de hipóteses, o nível de significância de um teste pode ser definido como:

• A.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• B.

  a máxima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é falsa;

• C.

  a mínima probabilidade admitida de se rejeitar a hipótese alternativa, dado que a hipótese nula é verdadeira;

• D.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese nula é verdadeira;

• E.

  a mínima probabilidade admitida de se rejeitar a hipótese nula, dado que a hipótese alternativa é verdadeira.

A tabela a seguir dá os valores de pares de observações (x_i, y_i ).

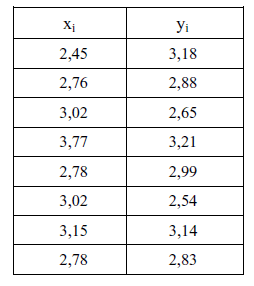
Para testar uma hipótese nula de que não há diferença entre as médias referentes à população X e à população Y, podemos usar o teste dos postos com sinal de Wilcoxon. O valor da estatística de teste para os dados apresentados pode ser:

• A.

  12

• B.

  14

• C.

  19

• D.

  24

• E.

  27

Deseja-se testar H₀: p = 1/2 contra H₁: p = 2/3, em que p é uma proporção populacional de "sucessos", com base numa amostra aleatória simples de tamanho 5 e com o critério que rejeita a hipótese nula de a proporção de "sucessos" na amostra for maior do que 70%. A probabilidade de se cometer erro tipo I com esse critério é:

• A.

  5/36;

• B.

  7/36;

• C.

  3/16;

• D.

  11/16;

• E.

  25/36.

Uma amostra aleatória simples de tamanho 100 será obtida de uma população normalmente distribuída com média μ desconhecida e variância 25. Para testar H0: μ ≥ 100 versus H1: μ < 100, o teste uniformemente mais poderoso de tamanho 0,05 rejeitará H0 se o valor da média amostral for:

• A.

  menor ou igual a 99,18;

• B.

  menor ou igual a 98,25;

• C.

  maior ou igual a 102,34;

• D.

  maior ou igual a 103,28;

• E.

  menor ou igual a 97,26.

NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.

Observe os testes abaixo (I, II, III e IV). Relacione se as afirmações sobre os mesmos são verdadeiras ou falsas e assinale a alternativa que contém a correlação correta.

• A.

  I _ V; II _ V; III _ F; IV _ F

• B.

  I _ F; II _ F; III _ V; IV _ V

• C.

  I _ F; II _ V; III _ F; IV _V

• D.

  I – V; II – F; III –V; IV – F

NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.

Com o objetivo de detetar contrabando de cocaína, cães farejadores são treinados. A Polícia Federal, desejando certificar-se da eficiência de tais treinamentos, resolveu submeter seus cães treinados a um teste. Esse teste consiste em detetar cocaína em duas malas: uma contendo a droga e a outra não. Após o teste realizado com 10 cães, selecionados aleatoriamente, 08 deles identificaram corretamente a mala que continha a droga. Considerando que para testar 0 1 : 0,5 Hπ= contra H:π > 0,5 e o nível de significância ser de 5 %, podemos afirmar que:

• A.

  se aceita que o treinamento dos cães é eficiente para deteção de cocaína, pois o valor de p é 0,055.

• B.

  não se pode evidenciar a eficiência do treinamento, pois estaríamos incorrendo um risco de 5,5%.

• C.

  se aceita que o treinamento dos cães é eficiente para deteção de cocaína, pois o risco do teste não ser eficiente é de apenas 4,4%.

• D.

  não se pode evidenciar a eficiência do treinamento, pois o valor de p é menor do que 0,05.

Um programa de controle de qualidade foi implementado em uma agência bancária. A cada 10 clientes que entram na fila para solicitar um certo tipo de serviço S, um atendente entrega um pequeno questionário, que deve ser preenchido pelo cliente e devolvido ao caixa do banco. Um dos quesitos monitorados diariamente é a proporção de clientes que estão satisfeitos com o atendimento de um modo geral. Em determinada semana, foram observados os resultados mostrados na tabela a seguir.

 Com base nesses dados, julgue os itens que se seguem.

Considere que se deseje testar a hipótese de que a verdadeira proporção de clientes satisfeitos na terça-feira seja superior a 0,85. Nessa situação, a estatística do teste, considerando a aproximação normal, é dada por

• C. Certo
• E. Errado

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

Sob a hipótese nula, a estatística do teste segue a distribuição t com 31 graus de liberdade.

• C. Certo
• E. Errado

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

Para o nível de significância de 2%, há evidências estatísticas suficientemente fortes para se rejeitar a hipótese de que as produtividades médias não são iguais.

• C. Certo
• E. Errado

Um banco deseja testar se a produtividade média de um grupo de empregados de determinado setor da agência I é igual à produtividade média de um outro grupo de empregados de um setor equivalente da agência II. A produtividade foi definida em função do número diário de contratos avaliados por cada empregado. Como as duas agências possuem características similares, foram coletadas amostras de igual tamanho (32 empregados), obtendo-se os resultados apresentados na tabela a seguir. Considere que as distribuições das produtividades de ambas as agências sejam normais com variâncias iguais.

Considere ainda que o teste t para a comparação da média de duas amostras independentes tenha sido aplicado. Dado que P(Z > 1,96) = 0,025 e P(Z > 2,326) = 0,01, em que Z é uma distribuição normal padrão, julgue os itens a seguir com base nessas informações.

O poder do teste é a probabilidade de a hipótese nula ser rejeitada, dado que, na realidade, as médias são iguais.

• C. Certo
• E. Errado