Questões sobre Teste de Hipótese

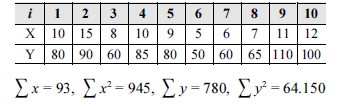
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

• C. Certo
• E. Errado

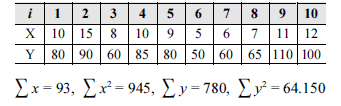
A fim de planejar o orçamento de uma grande empresa para o próximo ano, um analista selecionou uma amostra aleatória de 10 produtos (i) das empresas filiais e anotou as despesas (X) e os faturamentos (Y) totais decorrentes desses produtos (em R$ milhões). Os resultados por ele obtidos são mostrados na tabela acima.

Com base nessas informações, julgue os itens subsecutivos.

Considere um teste de hipóteses acerca da média da variável X. Nesse caso, se todos os demais momentos da distribuição X forem desconhecidos, então a estatística apropriada para esse teste segue uma distribuição t com 9 graus de liberdade.

• C. Certo
• E. Errado

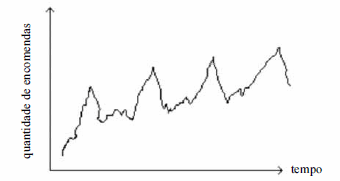
O gráfico acima mostra a evolução temporal da quantidade mensal de encomendas X entregues em determinada cidade. A partir dessa figura e dos conceitos de séries temporais, julgue os itens subsequentes.

Uma das suposições do modelo AR(p) é que os erros aleatórios sejam ruído branco.

• C. Certo
• E. Errado

Acerca de inferência estatística, julgue os itens de 75 a 85.

Suponha que se deseje testar H0 : θ = θ0 versus H1 : θ ≠ θ0, em que θ é um parâmetro populacional desconhecido e θ0 ∈ [φ1, φ2], em que [φ1, φ2] representa o intervalo de (1 – ") × 100% de confiança para θ. Nessa situação, se o nível de significância do teste for igual a " × 100%, a hipótese nula do teste em questão não será rejeitada.

• C. Certo
• E. Errado

A proporção de pessoas favoráveis a certo projeto governamental, em uma população, é p. Sorteiam-se 4 pessoas ao acaso e com reposição desta população e calcula-se a proporção pˆ de pessoas na amostra favoráveis ao projeto. Desejando-se testar H0: p = 0,5 versus H1: p = 0,7, decidiu-se rejeitar a hipótese nula se a região crítica do teste relativa a pˆ for {1}. Nessas condições, a probabilidade do erro do tipo II é

• A.

  0,7599

• B.

  0,7012

• C.

  0,5035

• D.

  0,3240

• E.

  0,2835

Seja X uma variável aleatória normalmente distribuída com média μ e variância populacional desconhecida. Deseja-se testar a hipótese em que a média μ da população, considerada de tamanho infinito, é superior a 20, ao nível de significância de 5%. Para testar a hipótese, foi extraída uma amostra aleatória de 9 elementos, apurando-se uma média igual a 21 e com a soma dos quadrados destes elementos igual a 3.987. As hipóteses formuladas foram H0: μ = 20 (hipótese nula) e H1: μ > 20 (hipótese alternativa). Utilizando o teste t de Student, obtém-se que o valor da estatística tc (t calculado), para ser comparado com o t tabelado, é igual a

• A.

  1,5.

• B.

  2,0.

• C.

  2,5.

• D.

  3,0.

• E.

  4,0.

Em um período, é realizada uma pesquisa com 150 passageiros escolhidos aleatoriamente em um grande aeroporto, detectandose que 60 deles são do sexo feminino. Com base nesta pesquisa, deseja-se testar a hipótese de que a proporção dos passageiros do sexo feminino é igual a dos passageiros do sexo masculino. Sendo p a proporção dos passageiros do sexo feminino, foram formuladas as hipóteses H0: p = 0,50 (hipótese nula) e H1: p ≠ 0,50 (hipótese alternativa), supondo normal a distribuição da frequência relativa dos passageiros do sexo feminino. Utilizando as informações da distribuição normal padrão (Z), em que as probabilidades P(Z > 1,96) = 2,5% e P(Z > 2,58) = 0,5%, é correto afirmar que H0

• A.

  não é rejeitada ao nível de significância de 5%.

• B.

  é rejeitada para qualquer nível de significância inferior a 5%.

• C.

  é rejeitada tanto ao nível de significância de 1% como de 5%.

• D.

  não é rejeitada para qualquer nível de significância inferior a 1%.

• E.

  é rejeitada para qualquer nível de significância superior a 1% e inferior a 5%.

• A.

  1 < r  2.

• B.

  2 < r  3.

• C.

  3 < r  4.

• D.

  4 < r  5.

• E.

  r > 5.

Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.

Uma metalúrgica produz blocos cilíndricos cujo diâmetro é uma variável aleatória X, com distribuição normal, média μ = 60 mm e desvio padrão σ = 9 mm. Os diâmetros de uma amostra de 9 blocos são medidos a cada hora, e a média da amostra é usada para decidir se o processo de fabricação está dentro dos padrões de qualidade exigidos. A regra de decisão envolvida no procedimento de qualidade é a seguinte: Se o diâmetro médio da amostra de 9 cilindros for superior a 64,5 mm ou inferior a 54 mm, o processo deve ser interrompido para ajustes; caso contrário o processo de fabricação continua. A probabilidade do processo parar desnecessariamente (isto é, parar quando a média μ e o desvio padrão σ permanecem sendo os valores acima citados) é de

• A.

  13,4%.

• B.

  12%.

• C.

  11,2%.

• D.

  10%.

• E.

  9%.

Com base na amostra observada, adotando-se um nível de significância de 5%, não há evidências estatísticas que permitem rejeitar a hipótese nula.

• C. Certo
• E. Errado