Questões de Estatística da Fundação CESGRANRIO (CESGRANRIO)

As técnicas de simulação são muito importantes em uma grande variedade de projetos quando estes apresentam cálculos muito complexos ou experimentos reais muito dispendiosos. Na base da simulação, tem-se a necessidade de geração de números pseudoaleatórios, quando as duas principais preocupações são: (1) um possível número deve ter a mesma probabilidade de ocorrer que qualquer outro dentre os demais possíveis números e (2) deve existir independência entre as ocorrências, isto é, a probabilidade de ocorrência de um número não deve ser afetada pelas eventuais ocorrências dos demais possíveis números. Os métodos de geração mais adotados na prática são: congruência mista (mixed congruential method), congruência multiplicativa (multiplicative congruential method) e congruência aditiva (additive congruential method). Considere os números inteiros K, L, M e N, tais que: 0 < K < M; 0 < L < M e N = 1, 2, 3... Para serem gerados números pseudoaleatórios entre 0 e M-1, iniciase com uma semente X₀ aleatoriamente escolhida e adota- se a relação de recorrência XN+1 = f(X_N, X_N-1, K, L)(módulo M), isto é, X_N+1 é o resto da divisão de f(X_N, X_N-1, K, L) por M. Nessas condições, quando

• A. f(XN, XN-1, K, L) = K.XN + L, tem-se a congruência mista.
• B. f(XN, XN-1, K, L) = K.XN / L, tem-se a congruência mista.
• C. f(XN, XN-1, K, L) = K.(XN + L), tem-se a congruência multiplicativa.
• D. f(XN, XN-1, K, L) = K.XN + L.XN-1, tem-se a congruência mista.
• E. f(XN, XN-1, K, L) = K.XN.XN-1, + L, tem-se a congruência multiplicativa.

Na simulação da operação de uma planta industrial, supõe- se que ela pode apresentar dois estados: ou operou normalmente ou operou com alguma anomalia. Se um dia operou normalmente, a probabilidade de apresentar alguma anomalia no dia seguinte é 70%. Quando um dia operou com alguma anomalia, a probabilidade de operar normalmente no dia seguinte é 60%. Independente de como esteja operando atualmente, após muitos dias de operação, a probabilidade de concluir um dia operando normalmente é de, aproximadamente,

• A. 42%
• B. 46%
• C. 51%
• D. 56%
• E. 60%

Com base em dados históricos, verifica-se que, se uma linha de produção apresenta um índice de falhas inferior a 5% em determinado dia, a probabilidade de operar com mesmo nível de qualidade no dia seguinte é de 80%. Por outro lado, se opera com índice de falhas igual ou superior a 5% em algum dia, a probabilidade de voltar a operar com índice inferior a 5% no dia seguinte é de, apenas, 30%. Se, na simulação desse processo, verifica-se que a probabilidade de estar operando com índice de falhas inferior a 5% em algum dia é de 70%, a probabilidade de assim estar operando dois dias depois é de

• A. 42%
• B. 46%
• C. 51%
• D. 56%
• E. 63%

• A. 9 h 22 min
• B. 9 h 23 min
• C. 9 h 24 min
• D. 9 h 25 min
• E. 9 h 26 min

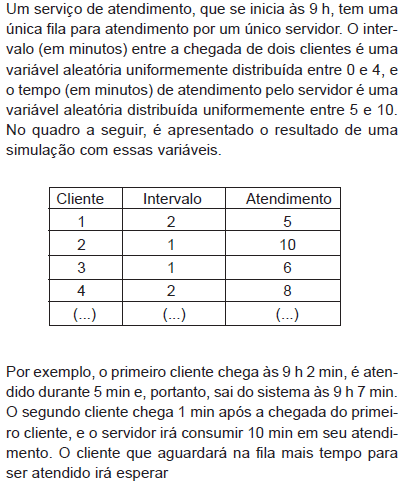
• A. 13 min
• B. 14 min
• C. 15 min
• D. 16 min
• E. 17 min

Três pessoas nasceram em abril. A probabilidade de que as três façam aniversário no mesmo dia é de

• A.

  1/3600

• B.

  1/2700

• C.

  1/900

• D.

  1/300

• E.

  1/30

Dois eventos de probabilidade positiva são disjuntos, isto é, não podem ocorrer simultaneamente. Em consequência,

• A.

  são eventos independentes.

• B.

  têm a mesma probabilidade.

• C.

  a soma de suas probabilidades é igual a 1.

• D.

  sua união tem probabilidade nula.

• E.

  sua intercessão tem probabilidade nula.

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Sendo X e Y duas variáveis aleatórias e E ( ) o operador esperança matemática, em geral, NÃO é correto que

• A.

  E (2 X) = 2 E(X)

• B.

  E (2 + X) = 2 + E(X)

• C.

  E (X + Y) = E(X) + E(Y)

• D.

  E(XY) = E(X) E(Y)

• E.

  E (2) + X = 2 + X

Um importante indicador da qualidade do modelo de regressão, obtido com a aplicação do Método dos Mínimos Quadrados, é o coeficiente de determinação, que é

• A. inversamente proporcional à variação explicada pela variável independente.
• B. inversamente proporcional à soma dos quadrados, devido à regressão.
• C. diretamente proporcional à variação explicada pela variável dependente.
• D. diretamente proporcional à variação explicada pela variável independente.
• E. diretamente proporcional à soma dos quadrados dos resíduos.