Questões de Estatística da Escola de Administração Fazendária (ESAF)

Em situações práticas de pesquisa em que existe um grande número de variáveis correlacionadas, é possível aplicar uma técnica de Análise Multivariada que busca reduzir o número de variáveis sem perder muito da informação contida na matriz de covariâncias. Para isso, as variáveis originais são transformadas obtendo-se novas variáveis com propriedades ótimas de variância. Assim, a primeira nova variável é a combinação linear normalizada das variáveis originais com máxima variância. A segunda nova variável é a combinação linear normalizada das variáveis originais, não correlacionada com a primeira nova variável e com máxima variância. A terceira nova variável é ainda a combinação linear normalizada das variáveis originais agora não correlacionada com a primeira e a segunda novas variáveis e com máxima variância e assim por diante. Essa técnica de Análise Multivariada é denominada:

• A. Análise Discriminante.
• B. Análise Fatorial.
• C. Correlação Canônica.
• D. Análise de Componentes Principais.
• E. Distribuição Normal Multivariada.

• A.
• B.
• C.
• D.
• E.

Os dados da Tabela abaixo ilustram o que uma empresa produz para uma determinada linha de produto. Estes dados foram anotados durante quatro meses consecutivos. Tomando como base 100 em março, o índice de produtividade de horas trabalhadas em maio é igual a:

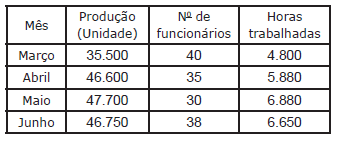
• A. 6,9
• B. 100
• C. 93,7
• D. 1590
• E. 80

Uma empresa da Indústria de chips deseja desenvolver um novo chip. Para o desenvolvimento deste novo chip, a empresa tem duas alternativas:

- alternativa 1: pesquisa e desenvolvimento (P&D) por sua própria conta;

- alternativa 2: desenvolver o chip por meio de um acordo com uma outra empresa de engenharia.

A tabela abaixo apresenta, em valor presente, os lucros esperados para os próximos 5 anos, dependendo da alternativa escolhida e do sucesso alcançado.

Com base em estudos de viabilidade e em estudos de diversas empresas de consultoria e de desenvolvimento, obteve-se as seguintes probabilidades para cada um dos estados da natureza: p1 = 0,2 (muito sucesso); p2 = 0,5 (razoável sucesso) e p3 = 0,3 (pouco sucesso). Portanto, a empresa deseja saber (em milhões de reais): qual o valor da decisão que corresponde ao Máximo Valor Esperado (MVE) e, qual o Ganho Esperado com Informação Perfeita (GEIP).

• A. MVE = 27 e GEIP= 12
• B. MVE = 40 e GEIP= 22
• C. MVE = 52 e GEIP= 22
• D. MVE = 27 e GEIP= 22
• E. MVE = 40 e GEIP= 12

Um banco possui um caixa para atendimento. Clientes que necessitam ser atendidos pelo caixa chegam de acordo com um processo de Poisson a uma taxa média de 9 por hora. Entretanto, se o caixa estiver ocupado (já atendendo um cliente), os possíveis novos clientes que chegarem poderão se recusar a esperar (poderão procurar outro banco para atendimento). Particularmente, se tivermos n clientes já no banco, a probabilidade de chegar um possível cliente que vai se recusar é de n/3 para n = 1, 2, 3. O tempo necessário para atender um cliente tem uma distribuição exponencial com uma média de quatro minutos. Portanto, o banco deseja saber qual é o tempo de espera previsto W (incluindo atendimento), para os clientes que decidem permanecer no banco.

• A. W=5,5 minutos
• B. W=10,5 minutos
• C. W=12 minutos
• D. W=3 minutos
• E. W=8 minutos

número médio de clientes na ofi cina (L), e o número médio de clientes esperando para serem atendidos para a troca de óleo (L_q) é dado por:

• A. L = 2,5 e L_q= 1,26.
• B. L = 3 e L_q= 1,32.
• C. L = 2 e L_q= 1,52.
• D. L = 2 e L_q= 1,12.
• E. L = 3 e L_q= 1,16.

• A.

  se x₁ aumentar em uma unidade, Y diminuirá de 2 unidades.

• B.

  x₁, x₂ e x₃ explicam as variações de Y em torno de sua média.

• C.

  84,32% das variações de Y em torno de sua média são explicadas por x₁, x₂ e x₃.

• D.

  x₁ e x₂ explicam as variações de Y em torno de sua média.

• E.

  a probabilidade de se cometer Erro Tipo II é igual a 90%.

Com relação aos índices de Laspeyres, Paasche e Fischer pode-se afi rmar que o número-índice de:

• A.

  Fischer é a média harmônica entre os índices de Laspeyres e de Paasche.

• B.

  Laspeyres é uma média harmônica ponderada de relativos.

• C.

  Paasche é uma média geométrica ponderada de relativos.

• D.

  Laspeyres é uma média ponderada de relativos.

• E.

  Fischer é a média aritmética entre os índices de Laspeyres e de Paasche.

Em um experimento, obteve-se uma amostra de 15 valores da variável discreta x. A amostra é dada pelo conjunto {1, 2, 3, 1, 3, 4, 3, 4, 3, 2, 3, 5, 2, 4, 5}. Assim, para esta amostra, a média aritmética, a moda, a mediana e o tipo de distribuição obtidas são, respectivamente:

• A.

  3, 5, 3, assimétrica positiva

• B.

  3, 5, 3, assimétrica negativa

• C.

  3, 5, 3, simétrica

• D.

  3, 3, 3, simétrica

• E.

  3, 3, 5, assimétrica negativa

Pelo valor do quociente entre o momento centrado de terceira ordem e o cubo do desvio padrão da distribuição de frequências apresentada na Questão 76, pode-se concluir que a distribuição

• A.

  é mesocúrtica.

• B.

  é simétrica.

• C.

  possui assimetria negativa.

• D.

  possui assimetria positiva.

• E.

  é leptocúrtica.