Questões de Estatística da Fundação Carlos Chagas (FCC)
Lista completa de Questões de Estatística da Fundação Carlos Chagas (FCC) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Relativamente à Análise Multivariada de Dados, considere as afirmativas abaixo.
I. A análise fatorial é um exemplo de técnica de interdependência, o que significa que nenhuma variável ou grupo de variáveis é definida como sendo dependente ou independente.
II. A análise de correlação canônica não é adequada se as variáveis independentes são quantitativas.
III. A análise discriminante múltipla é adequada se a única variável dependente for categórica.
IV. A análise de correspondência não é adequada para teste de hipóteses.
Está correto o que se afirma APENAS em
- A.
I e IV.
- B.
II e III.
- C.
I e III.
- D.
I, III e IV.
- E.
III e IV.
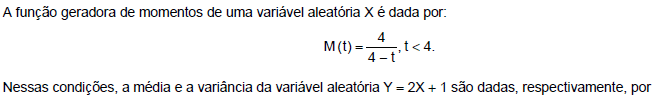
- A.
0,5 e 0,125.
- B.
1,5 e 0,25.
- C.
1,75 e 0,5.
- D.
0,5 e 0,25.
- E.
1,5 e 0,5.
Após o lançamento de um novo modelo de automóvel observou-se que 20% deles apresentavam defeitos na suspensão, 15% no sistema elétrico e 5% na suspensão e no sistema elétrico. Selecionaram-se aleatoriamente e com reposição 3 automóveis do modelo novo. A probabilidade de pelo menos dois apresentarem algum tipo de defeito é
- A.
0,354.
- B.
0,324.
- C.
0,316.
- D.
0,296.
- E.
0,216.

- A.
0,875.
- B.
0,895.
- C.
0,912.
- D.
0,944.
- E.
0,954.
A população correspondente aos salários dos empregados de um determinado ramo de atividade é considerada normal, de tamanho infinito e desvio padrão populacional igual a R$ 400,00. Uma amostra aleatória de tamanho 100 é extraída desta população obtendo-se uma média igual a R$ 2.050,00. Com base nesta amostra, deseja-se testar a hipótese se a média μ da população é igual a R$ 2.000,00, a um nível de significância de 5%. Foram formuladas as hipóteses Ho: μ = R$ 2.000,00 (hipótese nula) e H1: μ ≠ R$ 2.000,00 (hipótese alternativa). Para a tomada de decisão, o valor do escore reduzido, utilizado para comparação com o valor z da distribuição normal padrão (Z) tal que a probabilidade P (|Z| > z) = 5%, é
- A.
2,50.
- B.
2,25.
- C.
2,00.
- D.
1,75.
- E.
1,25.
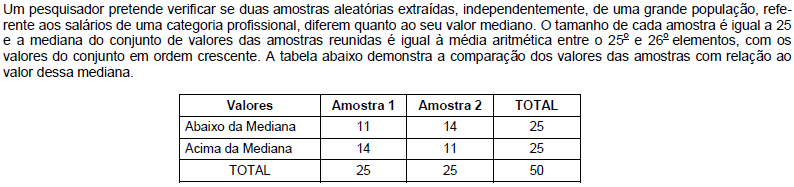
O pesquisador utilizou o teste da mediana para decidir se as medianas das duas amostras são iguais, ao nível de significância de 5%. As hipóteses formuladas foram Ho: As medianas são iguais (hipótese nula) e H1: As medianas são diferentes (hipótese alternativa), sabendo que ao nível de significância de 5% a variável qui-quadrado com 1 grau de liberdade é igual a 3,84. Então, uma conclusão correta é que Ho
- A.
não é rejeitada e o qui-quadrado observado é igual a 0,36.
- B.
é rejeitada e o qui-quadrado observado é igual a 0,36.
- C.
não é rejeitada e o qui-quadrado observado é igual a 0,72.
- D.
é rejeitada e o qui-quadrado observado é igual a 0,72.
- E.
não é rejeitada e o qui-quadrado observado é igual a 1,96.

Com relação aos valores destes salários, a soma da média aritmética com a mediana e com a moda é igual a
- A.
R$ 11.375,00.
- B.
R$ 10.875,00.
- C.
R$ 10.500,00.
- D.
R$ 10.375,00.
- E.
R$ 9.675,00.
Para resolver as questões de números 41 e 42 considere uma amostra aleatória com 10 pares de observações (Xi, Yi), i = 1, 2, . . ., 10. O objetivo é descrever Y como função linear de X por meio do modelo Yi = α + βXi + ∈i, sendo i a i-ésima observação, α e β são parâmetros desconhecidos e ∈i o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizando o método dos mínimos quadrados, obteve-se a e b, que são as estimativas de α e β, respectivamente. Verificou-se que a reta determinada pela função Y = a + bX passa pelos pontos (1, 8 ) e (4 , 2).
Se o valor da média das observações Yi é igual a 4,4; então, a média das observações Xi é
- A.
3,6.
- B.
3,2.
- C.
2,8.
- D.
2,4.
- E.
2,0.














