Questões de Estatística da Fundação Carlos Chagas (FCC)

• A.

  81.

• B.

  64.

• C.

  49.

• D.

  42.

• E.

  36.

A soma dos valores de todos os 50 elementos de uma população X é igual a 2.750. O coeficiente de variação para esta população apresenta o valor de 20%. Então, o valor da soma dos quadrados de todos os elementos de X é

• A.

  157.300.

• B.

  154.275.

• C.

  151.250.

• D.

  80.025.

• E.

  8.800.

É correto afirmar que

• A.

  

• B.

  

• C.

  

• D.

  E’ é mais consistente que E’’.

• E.

  E’’ é mais eficiente que E’.

Considere o modelo de séries temporais dado por Z_t = 0,6 Z_t−1 + a_t onde a_t é o ruído branco de média zero e variância 4. Nessas condições, a variância de Z_t é

• A.

  4,25.

• B.

  5,75.

• C.

  6,25.

• D.

  6,50.

• E.

  6,75.

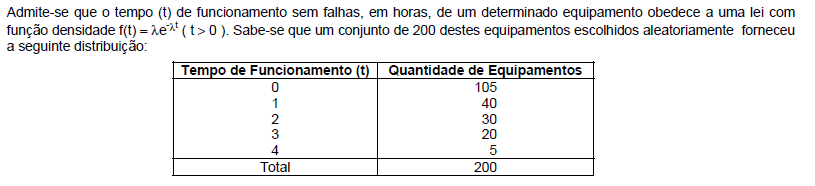
Utilizando o M¨¦todo dos Momentos, tem-se que o valor da estimativa de ¦Ë ¨¦ igual a

• A.

  9/5

• B.

  8/5

• C.

  9/8

• D.

  5/4

• E.

  10/9

igual

• A.

  0,80.

• B.

  1,20.

• C.

  1,60.

• D.

  2,00.

• E.

  2,40.

Sejam f(k), k=1,2,3,... e h(k), k=1,2,3,..., respectivamente, as funções de autocorrelação e autocorrelação parcial de um processo

I. f(k) ≠ 0, para k=1 e 2, e é igual a zero para outros valores de k.

II. h(k) é dominada por uma mistura de exponenciais e senoides amortecidas.

As características (I) e (II) nos levam a identificar para p e q, respectivamente, os valores

• A.

  2 e 1.

• B.

  1 e 1.

• C.

  0 e 2.

• D.

  2 e 0.

• E.

  2 e 2.

Atenção: Para resolver as questões de números 55 a 57, dentre informações dadas abaixo, utilize aquelas que julgar apropriadas. Se Z tem distribuição normal padrão, então: P(Z<0,5) = 0,691; P(Z < 1) = 0,841; P(Z<1,5) = 0,933; P(Z<2) = 0,977; P(Z<2,58) = 0,995.

Sabe-se que o tempo para a ocorrência de defeito em uma peça tem distribuição normal com média de 1200 dias e desvio padrão de 100 dias. O fabricante de tais peças oferece aos seus clientes uma garantia de g dias (ele substitui toda peça que durar g dias ou menos). O valor de g para que apenas 0,5% das peças sejam substituídas é, em dias, igual a

• A.

  742.

• B.

  768.

• C.

  856.

• D.

  942.

• E.

  967.

Em uma comunidade 10% de todos os adultos com mais de 60 anos têm certa doença. Um teste diagnostica corretamente 90% de todos os adultos com mais de 60 anos, como portadores da mesma e incorretamente 5% de todos aqueles que não têm a doença, como portadores da mesma. A probabilidade de um adulto com mais de 60 anos ter de fato a doença, sabendo que ele foi diagnosticado como portador da mesma é

• A.

  1/3

• B.

  2/3

• C.

  1/5

• D.

  2/5

• E.

  3/5

Um dado é viciado de tal modo que a probabilidade de ocorrer face par é duas vezes mais provável do que ocorrer face ímpar. O dado é lançado duas vezes independentemente. Considere os seguintes eventos: A = a soma dos pontos das faces é 6; B = o número da face do primeiro dado é menor do que 3. Nessas condições, a probabilidade de A, sabendo que ocorreu B, é

• A.

  5/27

• B.

  5/81

• C.

  27/81

• D.

  12/81

• E.

  8/27