Questões de Estatística da Fundação Carlos Chagas (FCC)

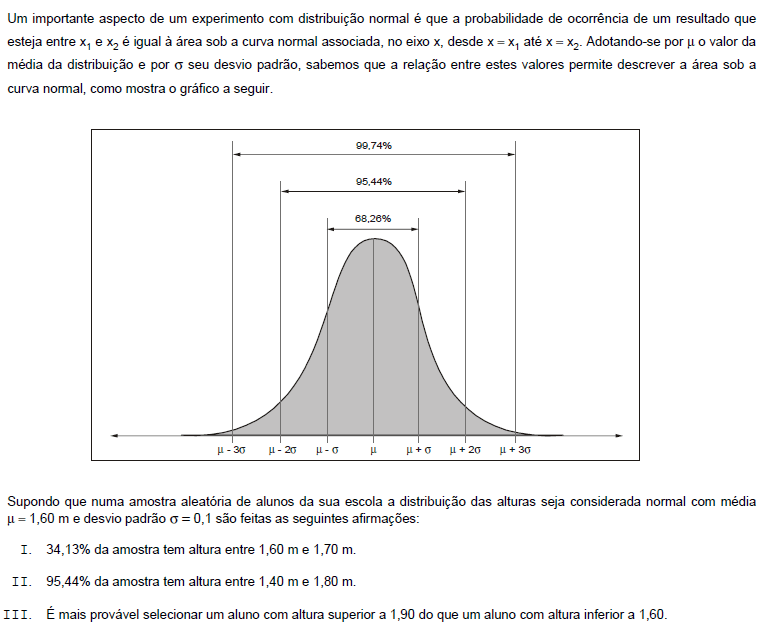
Com relação as afirmações acima podemos concluir que

• A.

  todas estão corretas.

• B.

  somente as afirmações I, II estão corretas.

• C.

  somente as afirmações II, III estão corretas.

• D.

  somente a afirmação I e III estão corretas.

• E.

  somente a afirmação I está correta.

A tabela abaixo descreve as cestas de produtos consumidos em duas épocas com os cálculos auxiliares.

Tomando como base a época 1 e calculando os índices no período de 1 a 2, tem-se que os números índices de Laspeyres de preços e Paasche para quantidades expressos em porcentagem são, respectivamente,

• A.

  130,70 e 128,00.

• B.

  128,00 e 130,70.

• C.

  131,25 e 128,00.

• D.

  128,00 e 131,25.

• E.

  131,25 e 130,70.

• A.

  Autocorrelação.

• B.

  Heterocedasticidade.

• C.

  Multicolinearidade.

• D.

  Anormalidade.

• E.

  Independência.

Um empresário espera, para o próximo exercício, obter os seguintes faturamentos brutos para a sua empresa em função dos cenários "Bom", "Médio" e "Ruim":

A variância do respectivo faturamento bruto, em (R$ 1.000,00)², é igual a

• A.

  12.900.

• B.

  16.810.

• C.

  18.100.

• D.

  17.900.

• E.

  16.500.

A média aritmética e a variância dos salários dos empre- gados em uma fábrica são iguais a R$ 1.500,00 e 22.500 (R$) ², respectivamente. Para todos os emprega- dos foi concedido um reajuste de 8% e posteriormente um adicional fixo de R$ 180,00. O coeficiente de variação, após o reajuste e o adicional concedidos, é igual a

• A.

  5%.

• B.

  6%.

• C.

  8%.

• D.

  9%.

• E.

  10%.

Em um teste de hipótese estatístico, sendo H₀ a hipótese nula e H₁ a hipótese alternativa, o nível de significância do teste consiste na probabilidade de

• A.

  aceitar H₀ dado que H₀ é verdadeira.

• B.

  rejeitar H₀ dado que H₀ é falsa.

• C.

  aceitar H₀, independentemente se H₀ é verdadeira ou falsa.

• D.

  aceitar H₀ dado que H₀ é falsa.

• E.

  rejeitar H₀ dado que H₀ é verdadeira.

Instruções: Para resolver às questões de números 39 e 40, considere a tabela de frequências relativas abaixo, que mostra a distribuição dos valores arrecadados, em 2008, sobre determinado tributo, referente a um ramo de atividade escolhido para análise. Sabe-se que:

I. As frequências absolutas correspondem às quantidades de recolhimentos, sendo as frequências relativas do segundo e terceiro intervalos de classe iguais a x e y, respectivamente.

II. A média aritmética da distribuição, valor arrecadado por recolhimento, é igual a R$ 3.350,00 (valor encontrado considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo).

A porcentagem de recolhimentos com valores arrecadados maiores ou iguais a R$ 3.000,00 é

• A.

  70%

• B.

  65%

• C.

  55%

• D.

  45%

• E.

  40%

Uma amostra com apenas 9 elementos foi extraída de uma população normal de tamanho infinito com variância desconhecida. A média amostral apresentou um valor igual a 10 com uma variância igual a 16. Um intervalo de confiança de 90% para a média foi obtido utilizando a distribuição t de Student, considerando t_0,05 o quantil da distribuição t de Student para teste unicaudal tal que P (t > t_0,05) = 0,05, com n graus de liberdade. O intervalo de confiança, utilizando os dados da amostra, é

• A.

  [7,37; 12,63]

• B.

  [7,41; 12,59]

• C.

  [7,47; 12,53]

• D.

  [7,52; 12,48]

• E.

  [7,56; 12,44]

Em uma região, suspeita-se que a escolha entre duas profissões P₁ e P₂ dependa do sexo das pessoas. Nenhuma pessoa pode exercer simultaneamente P₁ e P₂. Dentre as pessoas que exercem estas duas profissões, foram formados dois grupos, o primeiro com 80 homens e o segundo com 120 mulheres, obtendo-se o seguinte resultado:

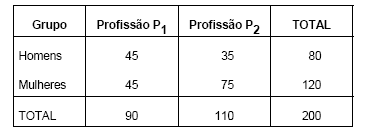
Utilizando o teste qui-quadrado a um nível de significância α tem-se que o valor crítico da distribuição qui-quadrado com 1 grau de liberdade é superior ao valor do qui-quadrado observado. Então, o valor do qui-quadrado observado e a conclusão com relação à escolha da profissão a um nível de significância α são

• A.

  6,818, depende do sexo.

• B.

  6,818, independe do sexo.

• C.

  8,045, depende do sexo.

• D.

  8,045, independe do sexo.

• E.

  6,250, depende do sexo.

Um partido político realizou um levantamento entre 100 filiados com relação à preferência entre dois candidatos, A e B, para um determinado cargo. Foram formados dois grupos, um com 60 homens e o outro com 40 mulheres.

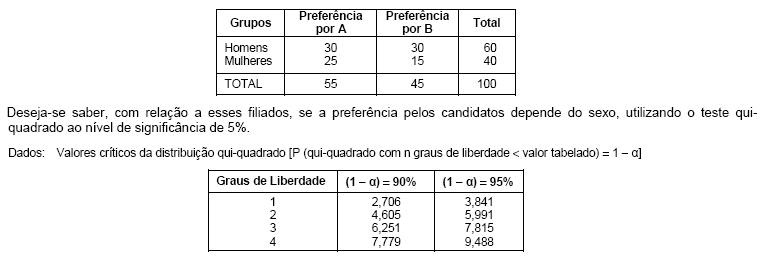
O valor do qui-quadrado observado e a respectiva conclusão é

• A.

  6,060; depende do sexo.

• B.

  4,545; depende do sexo.

• C.

  4,545; independe do sexo.

• D.

  1,515; depende do sexo.

• E.

  1,515; independe do sexo.