Questões de Estatística da Fundação Carlos Chagas (FCC)

Suponha que obteve-se uma amostra aleatória (X₁, X₂,...X_n) de uma variável aleatória X com função densidade de probabilidade

O estimador de máxima verossimilhança de λ é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O gerente de uma indústria de determinado componente eletrônico garante que a vida média do produto fabricado é igual a 100 horas. Um comprador desta indústria decide testar a afirmação do gerente e faz um teste estatístico formulando as hipóteses H₀: μ = 100 e H₁ : μ < 100, sendo que H₀ é a hipótese nula, H₁ é a hipótese alternativa e μ é a média da população considerada de tamanho infinito com uma distribuição normal. O desvio padrão populacional é igual a 10 horas e utilizou-se a informação da distribuição normal padrão (Z), segundo a qual a probabilidade P(Z ≥ 1,64) = 5%. H0 foi rejeitada com base em uma amostra aleatória de 64 componentes em um nível de significância de 5%. Então, o valor da média amostral foi, em horas, no máximo,

• A.

  94,75

• B.

  95,00

• C.

  96,00

• D.

  96,50

• E.

  97,95

Considere:

I. Dados demográficos incluem informações sobre uma população tais como a sua composição por sexo, raça e idade.

II. Estatísticas vitais lidam com nascimentos, mortes, casamentos, divórcios e ocorrências de doenças.

III. Em demografia, o conceito de taxa e de proporção têm o mesmo significado.

IV. Pirâmide etária é uma representação gráfica da composição da população de um lugar em função da idade e do sexo, em um determinado período de tempo.

Está correto o que se afirma APENAS em

• A.

  I e II.

• B.

  I, II e IV.

• C.

  II, III e IV.

• D.

  II e III.

• E.

  III e IV.

Considere as seguintes afirmações relativas às técnicas de Análise Multivariada:

I. Na análise de componentes principais a obtenção das componentes principais envolve a decomposição da matriz de covariâncias do vetor aleatório de interesse.

II. Na análise discriminante não é necessário que os grupos nos quais cada elemento amostral pode ser classificado sejam conhecidos à priori.

III. O escalonamento dimensional gera uma medida de ajuste denominada Stress que quanto mais próxima de 1 estiver melhor será o ajuste.

IV. Na análise de agrupamentos, para que se possa proceder ao agrupamento de elementos, é necessário se decidir à priori a medida de similaridade ou dissimilaridade que será usada.

Dentre essas afirmações citadas são verdadeiras SOMENTE

• A.

  I e III.

• B.

  I e IV.

• C.

  I, II e III.

• D.

  II, III e IV.

• E.

  II e IV.

• A.

  não justo de θ.

• B.

  consistente de θ.

• C.

  viesado de θ.

• D.

  eficiente de θ.

• E.

  viciado de θ.

Considere as seguintes afirmações:

I. A análise fatorial tem como objetivo descrever a variabilidade do vetor aleatório X de dimensão n x 1, em termos de m variáveis aleatórias (m < n) chamadas de fatores comuns e que estão relacionadas com o vetor X por meio de um modelo linear.

II. As técnicas de conglomerados hierárquicas são utilizadas em análise exploratória de dados com o intuito de identificar possíveis agrupamentos e o valor possível do número de grupos.

III. O escalonamento multidimensional é uma técnica multivariada para se examinar relações geométricas entre variáveis contínuas ou categóricas nominais.

IV. A análise de componentes principais consiste em se formar novas variáveis, que são combinações lineares das variáveis originais, e que devem ser correlacionadas entre si.

Está correto o que se afirma APENAS em

• A.

  I e II.

• B.

  I, II e IV.

• C.

  I e III.

• D.

  I e IV.

• E.

  II e III.

A distribuição de frequências relativas abaixo refere-se aos preços unitários de venda (em R$) de um determinado equipamento no mercado.

Utilizando o método da interpolação linear, o valor do terceiro quartil da distribuição é

• A.

  R$ 3.250,00.

• B.

  R$ 3.125,00.

• C.

  R$ 3.000,00.

• D.

  R$ 2.875,00.

• E.

  R$ 2.750,00.

O tempo de vida de um aparelho, em unidades de 1.000 horas, é uma variável aleatória X com distribuição exponencial com função densidade de probabilidade dada por

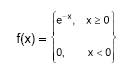
o custo de fabricação de um aparelho é R$ 500,00 e seu preço de venda é R$ 1.000,00. Sabendo que o fabricante garante a devolução do aparelho se x<0,2, o lucro esperado por aparelho, considerando que e^−0,2 = 0,820 , é

• A.

  320

• B.

  350

• C.

  370

• D.

  400

• E.

  420

Instruções: Para responder às questões de números 38 a 40 considere a tabela abaixo que mostra a distribuição de salários (em reais) dos funcionários de uma empresa. O valor da mediana, obtido por interpolação linear, é igual a R$ 2.900,00 e a frequência absoluta simples do terceiro intervalo de classe, igual a X.

O valor do terceiro quartil, obtido por interpolação linear, é igual a

• A.

  R$ 3.800,00

• B.

  R$ 3.750,00

• C.

  R$ 3.600,00

• D.

  R$ 3.500,00

• E.

  R$ 3.400,00

Considere a variável aleatória bidimensional (X,Y) cuja função densidade de probabilidade é dada por:

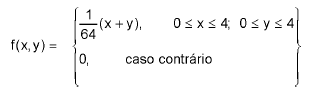
A esperança condicional de Y dado x, denotada por E(Y| x), é dada por

• A.

  

• B.

  

• C.

  

• D.

  

• E.