Questões de Estatística da Fundação Carlos Chagas (FCC)

Instruções: Para resolver às questões de números 59 e 60, utilize dentre as informações dadas a seguir, as que julgar necessárias. Se Z tem distribuição normal padrão, então:

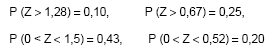
Sabe-se que, num município, impostos sobre imóveis , X, pagos por contribuintes, têm distribuição Normal com média μ e desvio padrão σ. Sabe-se que 30% dos impostos pagos são inferiores a R$ 1.200,00 e que 10% são superiores a R$ 3.000,00. O valor de μ e o valor do terceiro quartil da variável X, são dados, em reais, respectivamente, por

• A.

  1.670 e 2.300

• B.

  1.680 e 2.390

• C.

  1.700 e 2.420

• D.

  1.720 e 2.400

• E.

  1.720 e 2.390

Instruções: Para resolver às questões de números 59 e 60, utilize dentre as informações dadas a seguir, as que julgar necessárias. Se Z tem distribuição normal padrão, então:

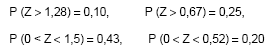
O custo de um produto é uma variável aleatória X com distribuição normal e sabe-se que este custo é a soma de três outros seguintes custos:

− custos fixos, que têm distribuição normal com média R$ 100,00 e desvio padrão R$ 20,00;

− custo da mão de obra, que tem distribuição normal com média R$ 500,00 e desvio padrão R$ 10,00;

− custo da matéria-prima, que é o dobro do custo da mão de obra.

Supondo que esses três custos sejam independentes, a probabilidade de X ser inferior a R$ 1.645,00 é

• A.

  0,93

• B.

  0,87

• C.

  0,85

• D.

  0,72

• E.

  0,64

• A.

  média 8 e variância 35.

• B.

  média 7 e variância 31.

• C.

  média 8 e desvio padrão 4.

• D.

  média 7 e desvio padrão 4.

• E.

  média 7 e variância 35.

Instruções: Para responder às questões de números 48 a 50 considere que uma empresa adotou o modelo Yi = α + βXi + εi, para prever o acréscimo da receita anual de vendas (com relação ao ano anterior) em função dos gastos com propagandas, com base em observações dos respectivos valores verificados nos últimos 10 anos.

Dados:

I. Y_i é o acréscimo da receita anual de vendas, em milhares de reais, no ano i.

II. X_i é o gasto com propagandas, também em milhares de reais, no ano i.

III. ε_i é o erro aleatório com as respectivas hipóteses consideradas para o modelo de regressão linear simples. IV. α e β são parâmetros desconhecidos.

V. Nos últimos 10 anos, o somatório dos acréscimos da receita anual de vendas e dos gastos com propaganda foram iguais a 1.200 e 200, respectivamente (valores em milhares de reais).

VI. Utilizou-se o método dos mínimos quadrados para a obtenção das estimativas de α e β com a respectiva equação da reta apresentando um coeficiente angular igual a 2,5

A previsão do acréscimo da receita anual de vendas em um determinado ano, caso a empresa opte por não gastar com propagandas é, em milhares de reais,

• A.

  70

• B.

  80

• C.

  90

• D.

  100

• E.

  120

Instruções: Para responder às questões de números 48 a 50 considere que uma empresa adotou o modelo Yi = α + βXi + εi, para prever o acréscimo da receita anual de vendas (com relação ao ano anterior) em função dos gastos com propagandas, com base em observações dos respectivos valores verificados nos últimos 10 anos.

Dados:

I. Y_i é o acréscimo da receita anual de vendas, em milhares de reais, no ano i.

II. X_i é o gasto com propagandas, também em milhares de reais, no ano i.

III. ε_i é o erro aleatório com as respectivas hipóteses consideradas para o modelo de regressão linear simples. IV. α e β são parâmetros desconhecidos.

V. Nos últimos 10 anos, o somatório dos acréscimos da receita anual de vendas e dos gastos com propaganda foram iguais a 1.200 e 200, respectivamente (valores em milhares de reais).

VI. Utilizou-se o método dos mínimos quadrados para a obtenção das estimativas de α e β com a respectiva equação da reta apresentando um coeficiente angular igual a 2,5

Utilizando a equação da reta obtida pelo método dos mínimos quadrados, em um ano que se deseja um acréscimo na receita anual de vendas de R$ 150.000,00, o gasto com propagandas terá que ser de, em milhares de reais,

• A.

  24

• B.

  30

• C.

  32

• D.

  36

• E.

  40

Instruções: Para responder às questões de números 48 a 50 considere que uma empresa adotou o modelo Yi = α + βXi + εi, para prever o acréscimo da receita anual de vendas (com relação ao ano anterior) em função dos gastos com propagandas, com base em observações dos respectivos valores verificados nos últimos 10 anos.

Dados:

I. Y_i é o acréscimo da receita anual de vendas, em milhares de reais, no ano i.

II. X_i é o gasto com propagandas, também em milhares de reais, no ano i.

III. ε_i é o erro aleatório com as respectivas hipóteses consideradas para o modelo de regressão linear simples. IV. α e β são parâmetros desconhecidos.

V. Nos últimos 10 anos, o somatório dos acréscimos da receita anual de vendas e dos gastos com propaganda foram iguais a 1.200 e 200, respectivamente (valores em milhares de reais).

VI. Utilizou-se o método dos mínimos quadrados para a obtenção das estimativas de α e β com a respectiva equação da reta apresentando um coeficiente angular igual a 2,5

Seja Y = f(X), em que f(X) é a função linear obtida pelo método dos mínimos quadrados. A relação 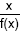 é igual a 20% quando X for igual a, em milhares de reais,

• A.

  50

• B.

  40

• C.

  36

• D.

  32

• E.

  28

Atenção: Para resolver às questões de números 40 a 42 considere as informações abaixo.

Considerando o quadro da análise de variância, obtém-se que o coeficiente de determinação (R²), definido como sendo o quociente da divisão da variação explicada devido à regressão pela variação total, é tal que

• A.

  R² < 93%.

• B.

  

• C.

  

• D.

  

• E.

  

Atenção: Para resolver às questões de números 40 a 42 considere as informações abaixo.

Para testar a existência da regressão, calcula-se o valor da estatística F_c (F calculado) para comparação com F_t tabelado (variável F de Snedecor com m graus de liberdade no numerador e n graus de liberdade no denominador). Os valores de (m + n), Fc e s² (estimativa da variância σ² do modelo teórico) são, respectivamente,

• A.

  10, 94 e 0,4000.

• B.

  9, 94 e 0,4000.

• C.

  9, 96 e 0,4125.

• D.

  8, 96 e 0,4125.

• E.

  8, 98 e 0,5625.

Atenção: Para resolver às questões de números 40 a 42 considere as informações abaixo.

Considere que In (e) = 1, In (6,34) = 1,8 e In (12) = 2,5. Desejando-se calcular o valor da previsão do empreendimento em 2010, em função da equação obtida, tem-se que esta previsão é igual a

• A.

  e^4,30

• B.

  e^6,66

• C.

  e^8,90

• D.

  e^11,17

• E.

  e^13,44

Atenção: Para resolver às questões de números 38 e 39 considere o texto abaixo. Uma amostra com 80 pares de observações (X_i, Y_i), i = 1, 2, 3, . . . , 80; sendo as somas das observações de X_i e Y_i iguais a 560 e 2.400, respectivamente. Um estudo tinha como objetivo analisar a relação entre X e Y e adotou-se o modelo Y_i = α + βX_i + ε_i, em que i corresponde a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados, com base na amostra, para o ajustamento do modelo obtendo-se para a estimativa de α o valor de 2.

Considerando a função linear obtida pelo método dos mínimos quadrados, tem-se que quando X varia de 1 unidade Y varia de

• A.

  2,0 unidades.

• B.

  2,5 unidades.

• C.

  3,0 unidades.

• D.

  3,5 unidades.

• E.

  4,0 unidades.