Questões de Estatística da Fundação Carlos Chagas (FCC)

Instruções: Para responder às questões de números 38 a 40 considere a tabela abaixo que mostra a distribuição de salários (em reais) dos funcionários de uma empresa. O valor da mediana, obtido por interpolação linear, é igual a R$ 2.900,00 e a frequência absoluta simples do terceiro intervalo de classe, igual a X.

Utilizando interpolação linear, tem-se que o número de funcionários que ganham salários menores ou iguais a R$ 3.700,00 é

• A.

  165

• B.

  166

• C.

  168

• D.

  170

• E.

  172

• A.

  1 e 2.

• B.

  2 e 1.

• C.

  3 e 2.

• D.

  3 e 4.

• E.

  1 e 4.

O gráfico abaixo demonstra a evolução da receita tributária anual no estado de São Paulo desde 1999, com os valores arrecadados em bilhões de reais.

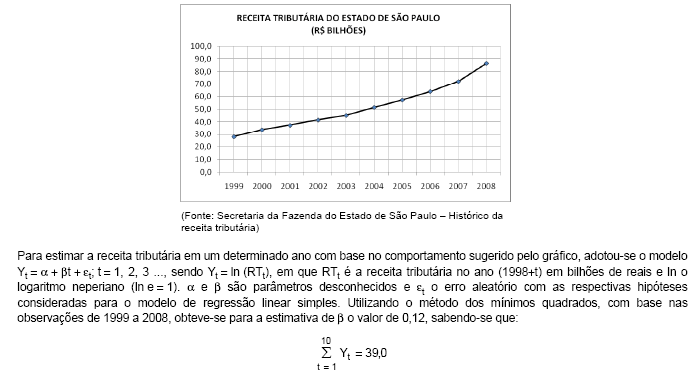
A previsão da receita tributária para 2009, em bilhões de reais, em função da equação obtida pelo método dos mínimos quadrados é igual a

• A.

  e^4,58

• B.

  e^4,56

• C.

  e^4,44

• D.

  e^4,32

• E.

  e^4,20

Uma variável aleatória U tem distribuição uniforme contínua no intervalo [α, β]. Sabe-se que a média de U é 1 e a variância é 1/12. O valor K, tal que P (X > K) = 0,25 é

• A.

  1,10

• B.

  1,15

• C.

  1,25

• D.

  1,29

• E.

  1,35

A distribuição dos salários dos 200 funcionários, em R$ 1.000,00, de determinada carreira profissional em um órgão público está representada pelo histograma abaixo. No eixo vertical estão assinaladas as respectivas densidades de frequências, em (R$ 1.000,00)−¹. Define-se densidade de frequência de um intervalo de classe como sendo o quociente da divisão da respectiva frequência relativa pela correspondente amplitude do intervalo.

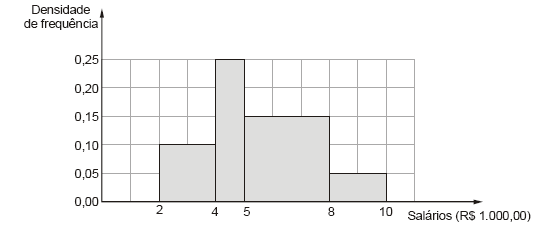
Considerando todos os intervalos de classe fechados à esquerda e abertos à direita, tem-se que a quantidade de funcionários que possuem salários maiores ou iguais a R$ 4.000,00 e inferiores a R$ 8.000,00 é

• A.

  60

• B.

  80

• C.

  90

• D.

  140

• E.

  160

Determinada carreira profissional em um órgão público apresenta 5 níveis de salários conforme demonstrado no eixo horizontal do gráfico abaixo. As colunas representam a quantidade de funcionários em cada nível.

Com relação aos valores das respectivas média aritmética (Me), mediana (Md) e moda (Mo), pode-se afirmar que

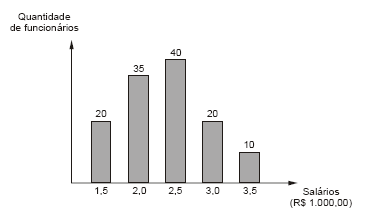
• A.

  Me = 2Md − Mo + R$ 860,00

• B.

  Me = Md + Mo − R$ 2.640,00

• C.

  Me = 3Md − 2Mo + R$ 1.360,00

• D.

  Me = Mo – Md + R$ 1.860,00

• E.

  Me = 2Mo − Md − R$ 360,00

Na análise de agrupamentos um critério para medir a distância entre dois objetos é denominado coeficiente de similaridade.

Seja:

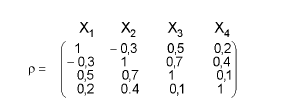
a matriz de correlação das variáveis X₁, X₂, X₃ e X₄.

 Usando como coeficiente de similaridade o coeficiente de correlação, as duas variáveis com comportamento mais parecido são:

• A.

  X₁ e X₂.

• B.

  X₁ e X₃.

• C.

  X₁ e X₄.

• D. X₂ e X₃.
• E.

  X₃ e X₄.

Espera-se que o número de reclamações tributárias em um órgão público durante determinada semana seja igual a 25, em qualquer dia útil. Sabe-se que nesta semana ocorreram 125 reclamações com a seguinte distribuição por dia da semana:

Para decidir se o número de reclamações tributárias correspondente não depende do dia da semana, a um nível de significância α, é calculado o valor do qui-quadrado (χ2) que se deve comparar com o valor do qui-quadrado crítico tabelado com 4 graus de liberdade. O valor de χ2 é

• A.

  1,20

• B.

  1,90

• C.

  4,75

• D.

  7,60

• E.

  9,12

Atenção: Para resolver às questões de números 56 e 57 use, dentre as informações dadas a seguir, as que julgar apropriadas. Se Z tem distribuição normal padrão, então:

P (Z > 1,64) = 0,05    P(Z > 2) = 0,02     P(0< Z < 1,75) = 0,46

Deseja-se estimar a proporção (p) de processos julgados por um tribunal regional do trabalho durante o período de 2000 até 2008. Uma amostra aleatória de 10.000 processos, selecionada da população (suposta infinita) de todos os processos, revelou que 5.000 foram julgados no referido período. Um intervalo de confiança, com coeficiente de confiança de 90% para p, baseado nessa amostra, é dado por

• A.

  0,5 ± 0,005

• B.

  0,5 ± 0,0062

• C.

  0,5 ± 0,0065

• D.

  0,5 ± 0,0082

• E.

  0,5 ± 0,01

Seja X uma variável aleatória representando a duração de vida de um equipamento. O desvio padrão populacional de X é igual a 20 horas. Uma amostra aleatória de 100 equipamentos forneceu uma duração de vida média igual a 1.000 horas obtendo-se um intervalo de confiança de 95% para a média populacional igual a [996,08 ; 1.003,92] (considerando a população normalmente distribuída e de tamanho infinito). Caso o tamanho da amostra tivesse sido de 400 e obtendo-se a mesma duração de vida média de 1.000 horas, o novo intervalo de confiança de 95% apresentaria uma amplitude de

• A.

  1,96 horas.

• B.

  2,94 horas.

• C.

  3,92 horas.

• D.

  5,88 horas.

• E.

  7,84 horas.