Questões de Estatística da Fundação Carlos Chagas (FCC)
Lista completa de Questões de Estatística da Fundação Carlos Chagas (FCC) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
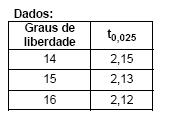
Os salários dos empregados de determinado ramo de atividade apresentam uma distribuição normal com uma variância populacional desconhecida. Uma amostra aleatória de 16 empregados deste ramo foi analisada apresentando uma média igual a R$ 1.500,00 e um desvio padrão igual a R$ 200,00. Considerando a população de tamanho infinito e t0,025 o quantil da distribuição t de Student para teste unicaudal tal que P(t > t0,025) = 0,025 com n graus de liberdade, obteve-se um intervalo de confiança de 95% para a média populacional. O intervalo obtido, com os valores em reais, foi igual a
- A.
[1.473,50; 1.526,50]
- B.
[1.473,00; 1.527,00]
- C.
[1.394,00; 1.606,00]
- D.
[1.393,50; 1.606,50]
- E.
[1.392,50; 1.607,50]
Seja uma variável aleatória X, tal que uma amostra aleatória de 5 elementos {100, 120, 180, 200, 240} foi extraída da população. O intervalo [120, 200] refere-se a um intervalo de confiança encontrado para a mediana de X. O nível de confiança deste intervalo é de
- A.
93,75%.
- B.
68,75%.
- C.
62,50%.
- D.
60,25%.
- E.
58,75%.
O diretor de uma empresa está convencido de que o desempenho dos funcionários com nível superior em sua empresa depende da faculdade em que eles se formaram. Resolve então promover um teste estatístico com 80 funcionários com nível superior utilizando o quadro abaixo, levando em conta que qualquer funcionário formou-se em uma e somente uma das faculdades (X, Y ou Z).
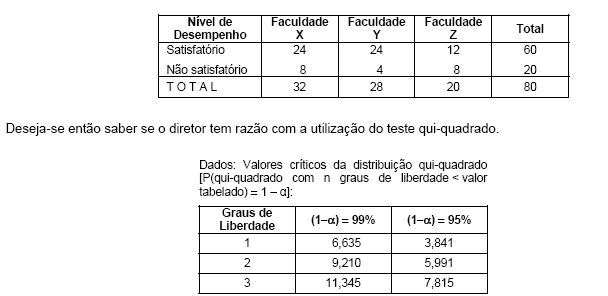
Uma respectiva conclusão é que
- A.
o diretor somente tem razão para um nível de significância superior a 1% e inferior a 5%.
- B.
não existe um nível de significância tal que o diretor tenha razão.
- C.
o diretor tem razão ao nível de significância de 5%, mas não ao nível de 1%.
- D.
tanto ao nível de significância de 1% como ao nível de 5% o diretor não tem razão.
- E.
existe um nível de significância inferior a 1% tal que o diretor tem razão.
A duração de vida de um determinado equipamento apresenta uma distribuição normal com uma variância populacional igual a 100 (dias)2. Uma amostra aleatória de 64 desses equipamentos forneceu uma média de duração de vida de 1.000 dias. Considerando a população de tamanho infinito, um intervalo de confiança de (1 − α) com amplitude de 4,75 dias para a média foi construído. Caso o tamanho da amostra tivesse sido de 400, obtendo-se a mesma média de 1.000 dias, a amplitude do intervalo de confiança de (1 − α) seria de
- A.
0,950 dias.
- B.
1,425 dias.
- C.
1,900 dias.
- D.
2,375 dias.
- E.
4,750 dias.
Em uma cidade com uma grande quantidade de eleitores, certo candidato encomenda uma pesquisa visando verificar qual será a proporção de votos a seu favor, estabelecendo que o erro amostral da proporção seja no máximo 2%. Para a pesquisa considerou-se normal a distribuição amostral da frequência relativa dos eleitores que manifestaram seu interesse em votar no candidato e que na distribuição normal padrão (Z) a probabilidade P (|Z|≤ 1,8) = 93%. O resultado da pesquisa apresentou uma variância com valor máximo e com um intervalo de confiança de 93%. O tamanho da amostra foi então de
- A.
8.000
- B.
5.000
- C.
4.000
- D.
2.500
- E.
2.025

- A.
−0,75 e 0,75
- B.
0,5 e 0,5
- C.
−0,5 e 0,25
- D.
−0,5 e 0,75
- E.
−1 e 0,5

- A.

- B.

- C.

- D.

- E.

Considere a variável aleatória bidimensional (X, Y) com função densidade conjunta dada por:

onde e é a base dos logaritmos naturais.
A esperança condicional de X dado y, denotada por E(X/y) é dada por
- A.

- B.
e
- C.

- D.

- E.

Uma variável aleatória X, com variância igual a 4, apresenta uma distribuição simétrica com relação à sua média com valor igual a 20. Utilizando o Teorema de Tchebyshev, a probabilidade mínima de que X pertença ao intervalo (10, 25) é igual a
- A.
72%
- B.
80%
- C.
84%
- D.
90%
- E.
96%
Instruções: Para responder às questões de números 37 a 39 considere a distribuição de frequências relativas acumuladas abaixo, correspondente aos salários dos 400 empregados de uma empresa no mês de setembro de 2009 (K > 0):
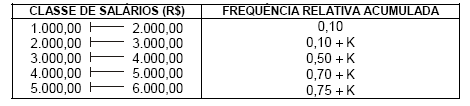
O valor da mediana dos salários dos empregados, obtido pelo método da interpolação linear, é igual a
- A.
R$ 3.250,00
- B.
R$ 3.375,00
- C.
R$ 3.450,00
- D.
R$ 3.600,00
- E.
R$ 3.750,00


