Questões de Estatística da Fundação Carlos Chagas (FCC)

Atenção: Para resolver às questões de números 38 e 39 considere o texto abaixo. Uma amostra com 80 pares de observações (X_i, Y_i), i = 1, 2, 3, . . . , 80; sendo as somas das observações de X_i e Y_i iguais a 560 e 2.400, respectivamente. Um estudo tinha como objetivo analisar a relação entre X e Y e adotou-se o modelo Y_i = α + βX_i + ε_i, em que i corresponde a i-ésima observação, α e β são parâmetros desconhecidos e εi o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples. Utilizou-se o método dos mínimos quadrados, com base na amostra, para o ajustamento do modelo obtendo-se para a estimativa de α o valor de 2.

Se Y = f(X), em que f(X) é a função linear obtida pelo método dos mínimos quadrados, então a função Z, tal que Z = XY, atinge o valor mínimo quando X for igual a

• A.

  −0,75.

• B.

  −0,50.

• C.

  −0,25.

• D.

  0,00.

• E.

  0,25.

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

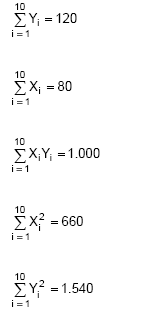
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

Utilizando a equação da reta obtida pelo método dos mínimos quadrados, tem-se que o menor valor inteiro X tal que o valor estimado de Y seja superior a 10 é

• A.

  5

• B.

  6

• C.

  7

• D.

  8

• E.

  9

Considere uma curva de uma distribuição estatística unimodal apresentando o valor da mediana superior ao valor da moda e o valor da média aritmética superior ao valor da mediana. Então, com relação às medidas de assimetria e curtose é correto afirmar que se trata de uma curva apresentando uma distribuição

• A.

  leptocúrtica.

• B.

  platicúrtica.

• C.

  assimétrica à esquerda.

• D.

  assimétrica à direita.

• E.

  com coeficiente de curtose igual ao da curva normal.

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

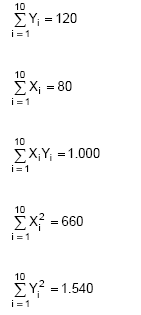
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

O valor da estimativa S² da variância do modelo teórico, baseado nos dados fornecidos, é

• A.

  1,2500

• B.

  1,5625

• C.

  1,8750

• D.

  2,1250

• E.

  2,5000

Instruções: Para responder às questões de 52 a 54 considere uma amostra aleatória de 10 pares de observações (Xi, Yi), i = 1, 2, 3, ..., 10 em que

 

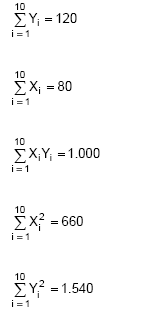
Obteve-se a partir do método dos mínimos quadrados o ajustamento do modelo Y1 = α + β X1 + εi em que α e β são parâmetros desconhecidos e εi o erro aleatório, com as respectivas hipóteses consideradas para a regressão linear simples.

Seja F_c o valor da estatística F (F calculado) utilizado para comparação com o F tabelado (variável F de Snedecor com m graus de liberdade no numerador e n graus de liberdade no denominador, ao nível de significância α) para testar a existência da regressão. Então,

• A.

  F_c = 80 e  = 8

• B.

  F_c = 32 e mn = 8

• C.

  F_c = 80 e (m + n) = 10

• D.

  F_c = 32 e (m + n) = 10

• E.

  F_c = 80 e (m + n) = 9

Uma população possui 15 elementos e tem variância σ². Desta população retira-se uma amostra aleatória sem reposição de n elementos. Sabendo-se que a média amostral 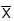 desses n elementos tem variância igual a  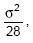, o valor de n é dado por

• A.

  5

• B.

  10

• C.

  14

• D.

  25

• E.

  28

Um levantamento realizado em duas empresas X e Y proporcionou os resultados apresentados na tabela abaixo.

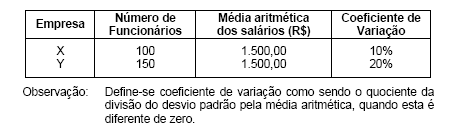
A variância dos salários das duas empresas reunidas é, em (R$)², igual a

• A.

  112.500.

• B.

  87.750.

• C.

  75.375.

• D.

  63.000.

• E.

  57.600.

A função de distribuição acumulada da variável aleatória X é dada por:

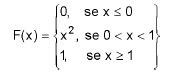
O valor da variância de X é

• A.
• B.

  

• C.

  

• D.

  

• E.

  

Uma variável aleatória X apresenta uma média igual a 8 e variância 25. Define-se variância relativa de uma variável aleatória como sendo a divisão da respectiva variância pelo valor do quadrado da média, quando esta é diferente de zero. Então, a variância relativa da variável aleatória Y = 2X – 1 é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O maior valor apresentado em uma amostra de 10 elementos de uma distribuição uniformemente distribuída sobre o intervalo [0, λ] é 2. O estimador de máxima verossimilhança da variância da população é

• A.

  

• B.

  

• C.

  1

• D.

  

• E.