Questões de Estatística da Fundação Carlos Chagas (FCC)

A média aritmética dos salários dos empregados de uma empresa X supera em R$ 350,00 a média aritmética dos empregados de uma outra empresa Y. Os correspondentes coeficientes de variação das empresas X e Y são iguais a 12,5% e 12%, respectivamente. Se a soma dos desvios padrões dos salários das duas empresas é igual a R$ 350,00, então a soma dos valores das médias aritméticas dos salários das duas empresas é

• A.

  R$ 3.500,00

• B.

  R$ 3.350,00

• C.

  R$ 2.850,00

• D.

  R$ 2.650,00

• E.

  R$ 2.550,00

Considere um teste estatístico envolvendo uma população normalmente distribuída em que se deseja testar, com relação a um parâmetro da distribuição, a hipótese nula (H₀) contra a hipótese alternativa (H₁), ao nível de significância α. Seja β a probabilidade de aceitar H₀ quando H₀ for falsa. Então,

• A.

  β corresponde ao erro tipo I ou erro de primeira espécie.

• B.

  α > β.

• C.

  α = 1− β.

• D.

  a região crítica do teste é determinada em função de β.

• E.

   corresponde à probabilidade de rejeitar H₀ quando H₀ for verdadeira.

Atenção: Para resolver às questões de números 32 e 33 considere a tabela de frequências relativas abaixo que demonstra a distribuição dos salários dos funcionários de uma empresa em julho de 2009.

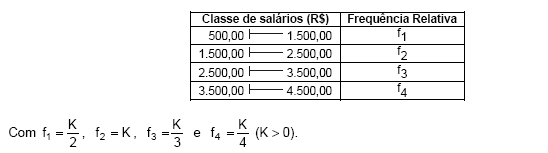
A média aritmética dos salários dos funcionários da empresa (valor calculado considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo) é, em reais, igual a

• A.

  4.000 K

• B.

  4.200 K

• C.

  4.400 K

• D.

  4.500 K

• E.

  4.800 K

Uma experiência consiste em verificar se uma moeda é honesta. Em 10 lançamentos da moeda, decide-se pela honestidade da moeda se o número de caras (n) for tal que 4 ≤ n ≤ 6 . A probabilidade de rejeitar a hipótese da moeda ser honesta, quando ela for correta é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Considere uma população que apresenta uma distribuição de Poisson tal que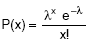e−λ com parâmetro λ desconhecido e x o número de ocorrências de um determinado acontecimento. Dessa população extraiu-se uma amostra aleatória com reposição de tamanho quatro (X1, X2, X3, X4) e utilizaram-se os dois estimadores seguintes para estimar a média (μ) da população:

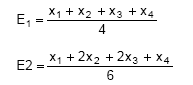
Então, com relação a estes 2 estimadores,

• A.

  E₁ é mais eficiente que E₂.

• B.

  E₁ e E₂ são consistentes.

• C.

  Apenas E₂ é enviesado.

• D.

  Apenas E₁ é não justo.

• E.

  E₂ é viciado.

Em uma cidade é realizada uma pesquisa sobre a preferência dos eleitores com relação a um determinado candidato, que afirma ter 60% da preferência. Uma amostra aleatória de tamanho 600 foi extraída da população, considerada de tamanho infinito, sendo que 330 eleitores manifestaram sua preferência pelo candidato. Com base nesta amostra, deseja-se testar a hipótese H₀ : p = 60% (hipótese nula) contra H₁ : p ≠ 60% (hipótese alternativa), em que p é a proporção dos eleitores que têm preferência pelo candidato. Para a análise considerou-se normal a distribuição amostral da frequência relativa dos eleitores que têm preferência pelo candidato e que na distribuição normal padrão Z a probabilidade P(|Z| ≤ 1,96) = 95% e P(|Z| ≤ 2,58) = 99%. A conclusão é que H0

• A.

  não é rejeitada tanto ao nível de significância de 1% como ao nível de significância de 5%.

• B.

  é rejeitada ao nível de significância de 5%.

• C.

  é rejeitada ao nível de significância de 1%.

• D.

  não é rejeitada para algum nível de significância superior a 5%.

• E.

  é rejeitada para algum nível de significância inferior a 1%.

Num certo bairro da cidade de Fortaleza, as companhias de seguro estabeleceram o seguinte modelo para o número de veículos furtados por semana:

O número médio de veículos furtados por semana é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

O gerente de produção de uma grande fábrica de farinha garante à sua rede de atacadistas que cada pacote produzido não contém menos de 1 kg de farinha. Um comprador desconfiado extrai uma amostra aleatória de 25 pacotes e encontra para esta amostra uma média m, em kg, e uma variância de 0,04 (kg)2. Supondo que a quantidade de farinha em cada pacote apresente uma distribuição normal com média μ e variância σ2 desconhecida, deseja-se saber se o gerente tem razão a um nível de significância de 5% com a realização do teste t de Student. Seja H0 a hipótese nula do teste (μ = 1 kg), H₁ a hipótese alternativa (μ < 1 kg) e t o valor do quantil da distribuição t de Student tal que P(|t| ≥ 1,71) = 0,05, tanto para 24 como para 25 graus de liberdade. Sabendo-se que H₀ foi rejeitada, então o valor encontrado para m foi, no máximo,

• A.

  0,8584 kg.

• B.

  0,8950 kg.

• C.

  0,9316 kg.

• D.

  0,9589 kg.

• E.

  0,9863 kg.

Em um município com 5.000 eleitores que trabalham, verificou-se que uma parte deles ganha, cada um, no máximo um salário mensal igual a R$ 1.000,00, sendo que a média aritmética destes apresentou um valor igual a R$ 500,00. A média aritmética dos salários dos eleitores que ganham acima de R$ 1.000,00 apresentou um valor igual a R$ 1.500,00. Se a média aritmética dos salários de todos estes 5.000 eleitores é igual a R$ 700,00, o número de eleitores que ganham acima de R$ 1.000,00 é

• A.

  1.000

• B.

  1.500

• C.

  2.000

• D.

  2.200

• E.

  2.400

O dirigente de uma empresa deverá decidir entre dois candidatos, Antônio e Paulo, qual ocupará o cargo de gerente administrativo. Para cada candidato foi aplicada uma mesma prova constituída de 16 testes de assuntos diversos. Subtraindo dos escores apresentados por Antônio os respectivos escores apresentados por Paulo, observa-se a presença de sinal negativo nas diferenças dos escores de 4 testes e sinal positivo nas 12 restantes, não ocorrendo diferença nula. Aplica-se o teste dos sinais para decidir se a proporção populacional de sinais negativos (p) é igual a 0,50, ao nível de significância de 2α, considerando as hipóteses: H₀ : p = 0,50 (hipótese nula) e H₁ : p ≠ 0,50 (hipótese alternativa). Aproximando a distribuição binomial pela normal, obteve-se o escore reduzido r correspondente para comparação com o valor crítico z da distribuição normal padrão (Z) tal que P(|Z| ≤ z) = 2α. Então,

• A.

  r = −2,00.

• B.

  r = −0,80.

• C.

  r = 0,50.

• D.

  r = 0,80.

• E.

  r = 2,00.