Questões de Estatística da Fundação Carlos Chagas (FCC)

Uma população finita com n (n > 1) valores estritamente positivos X₁, X₂, X₃, ..., X_n ; correspondente a um determinado atributo, possui média aritmética M₁ e variância V₁. Um dos valores da população é igual a M₁ e ele é retirado do conjunto. Então, com relação aos novos valores da média aritmética (M₂) e da variância (V₂), é correto afirmar que

• A.

  M₂ = M₁ e V₂ = V₁

• B.

  

• C.

  

• D.

  

• E.

  

Instruções: Para resolver às questões de números 39 e 40, considere a tabela de frequências relativas abaixo, que mostra a distribuição dos valores arrecadados, em 2008, sobre determinado tributo, referente a um ramo de atividade escolhido para análise. Sabe-se que:

I. As frequências absolutas correspondem às quantidades de recolhimentos, sendo as frequências relativas do segundo e terceiro intervalos de classe iguais a x e y, respectivamente.

II. A média aritmética da distribuição, valor arrecadado por recolhimento, é igual a R$ 3.350,00 (valor encontrado considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo).

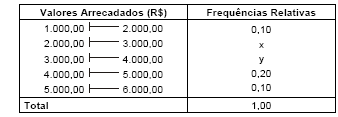
Utilizando o método da interpolação linear, tem-se que o valor da respectiva mediana é

• A.

  R$ 3.120,00

• B.

  R$ 3.200,00

• C.

  R$ 3.400,00

• D.

  R$ 3.600,00

• E.

  R$ 3.800,00

Considere que houve interesse em comparar a eficácia de 3 métodos de treinamento para uma profissão e que os candidatos foram escolhidos por sorteio e divididos em 3 grupos, com 10 elementos cada um.

− GRUPO I: recebeu treinamento à distância, pela Internet.

− GRUPO II: recebeu treinamento no local de trabalho com instrutor.

− GRUPO III: recebeu treinamento por instrução programada.

Após o término dos 3 métodos de treinamento, foi aplicado um teste com notas variando de 0 a 10 para todos os candidatos. Pelo quadro de análise de variância, obteve-se os seguintes resultados com relação às notas apresentadas pelos candidatos:

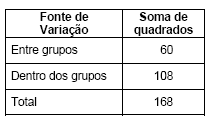
Para testar a hipótese da existência de reais diferenças na eficácia dos métodos foi calculado o valor da estatística F para comparação com o F tabelado (variável F de Snedecor com m graus de liberdade no numerador e n graus de liberdade no denominador). O valor calculado da estatística F foi de

• A.

  4,0.

• B.

  4,5.

• C.

  5,0.

• D.

  6,0.

• E.

  7,5.

Uma fábrica produz peças, das quais 90% são boas. As demais possuem algum tipo de defeito que não as inutiliza para o uso. As peças são vendidas em caixas com 2 peças. Se a caixa não tiver nenhuma peça defeituosa, seu preço de venda é R$ 200,00, tendo uma peça defeituosa o preço é R$ 100,00 e tendo mais de uma, o preço é R$ 50,00. O preço médio de uma caixa é

• A.

  R$ 180,50

• B.

  R$ 172,00

• C.

  R$ 168,50

• D.

  R$ 162,50

• E.

  R$ 161,00

A proporção de pessoas favoráveis a um certo projeto governamental é p. Sorteiam-se ao acaso, e com reposição, 400 pessoas. Calcula-se a proporção pˆ de pessoas favoráveis ao projeto na amostra. Deseja-se testar:

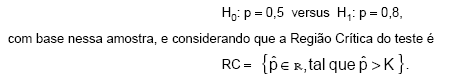
Fazendo uso do Teorema do Limite Central, o valor de K para que a probabilidade do erro tipo I seja igual à probabilidade do erro tipo II é

• A.

  4/5

• B.

  3/5

• C.

  5/6

• D.

  2/3

• E.

  5/8

De uma população com 500 famílias, tomou-se uma amostra casual simples de 30 famílias, para as quais foram observadas as seguintes variáveis:

X = número de pessoas na família.

Y = gasto mensal com alimentação.

• A.

  30.000

• B.

  36.000

• C.

  38.000

• D.

  40.000

• E.

  48.000

Considere a função densidade de probabilidade da variável X dada por:

Para testar as hipóteses

H0: φ = 1 versus H1: φ = 2, com base numa única observação, decidiu-se rejeitar H0 se X ≤ 0,8. Supondo que o valor observado para x foi 0,4, o nível descritivo e o poder do teste são dados respectivamente por

• A.

  (0,4)⁴ e 0,64

• B.

  (0,4)² e 0,8

• C.

  (0,4)³ e 0,64

• D.

  (0,4)⁴ e 0,8

• E.

  0,4 e 0,8

A probabilidade de que um cliente de banco, escolhido aleatoriamente, participe de um fundo multimercado promovido pelo banco é 0,20. Se cinco clientes são escolhidos aleatoriamente e com reposição, a probabilidade de que a proporção de participantes seja exatamente 0,40 é

• A.

  0,0816

• B.

  0,1048

• C.

  0,1280

• D.

  0,1850

• E.

  0,2048

Determinados processos de um tribunal são encaminhados para a análise de 3 analistas: X, Y e Z. Sabe-se que 30% de todos esses processos são encaminhados para X, 45% para Y e 25% para Z. Usualmente, por falta de documentação, uma parcela de tais processos é devolvida. Sabe-se que 5% , 10% e 10% dos processos de X, Y e Z, respectivamente, são devolvidos. A probabilidade de que um processo escolhido ao acaso tenha sido encaminhado para X, sabendo que foi devolvido, é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

A média aritmética e a variância dos salários dos empregados da empresa Gama são R$ 1.500,00 e 1.600,00 (R$)2, respectivamente. Como a distribuição destes salários é desconhecida, utilizou-se o teorema de Tchebyshev para saber qual é a proporção de empregados com salários inferiores ou iguais a R$ 1.400,00 ou salários superiores ou iguais a R$ 1.600,00. Esta proporção é no máximo

• A.

  25%

• B.

  16%

• C.

  10%

• D.

  8%

• E.

  4%