Questões de Estatística da Fundação Carlos Chagas (FCC)

O objetivo de uma pesquisa era o de se obter, relativamente aos moradores de um bairro, informações sobre duas variáveis: nível educacional e renda familiar. Para cumprir tal objetivo, todos os moradores foram entrevistados e arguídos quanto ao nível educacional, e, dentre todos os domicílios do bairro, foram selecionados aleatoriamente 300 moradores para informar a renda familiar. As abordagens utilizadas para as variáveis nível educacional e renda familiar foram, respectivamente,

• A.

  censo e amostragem por conglomerados.

• B.

  amostragem aleatória e amostragem sistemática.

• C.

  censo e amostragem casual simples.

• D.

  amostragem estratificada e amostragem sistemática.

• E.

  amostragem sistemática e amostragem em dois estágios.

Seja a distribuição binomial 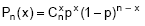 com parâmetro p desconhecido e x o número de ocorrências de um determinado acontecimento em n provas independentes. Se em 6 provas independentes o acontecimento A ocorreu 3 vezes e em 10 provas independentes o acontecimento A ocorreu 4 vezes, então a estimativa de p pelo método da máxima verossimilhança é

• A.

  45,00%.

• B.

  43,75%.

• C.

  42,00%.

• D.

  40,25%.

• E.

  40,00%.

Com relação à teoria geral de amostragem, considere as afirmativas abaixo.

I. A realização de amostragem aleatória simples só é feita para amostragem sem reposição.

II. A amostragem estratificada consiste na divisão de uma população em grupos segundo alguma característica conhecida. Os estratos da população devem ser mutuamente exclusivos.

III. Em uma amostra por conglomerados a população é dividida em subpopulações distintas.

IV. A amostragem sistemática é um plano de amostragem não probabilístico.

É correto o que se afirma APENAS em

• A.

  I e II.

• B.

  II e III.

• C.

  II e IV.

• D.

  III e IV.

• E.

  I, II e III.

Atenção: O enunciado abaixo refere-se às questões de números 41 e 42.

A tabela apresenta a classificação segundo duas variáveis, sexo e idade, dos 1.200 funcionários de uma empresa.

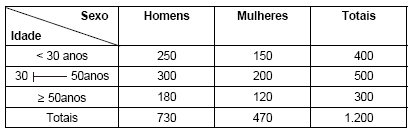
Se um funcionário é selecionado ao acaso dessa empresa, a probabilidade dele ser mulher ou ter pelo menos 30 anos é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Atenção: O enunciado abaixo refere-se às questões de números 41 e 42.

A tabela apresenta a classificação segundo duas variáveis, sexo e idade, dos 1.200 funcionários de uma empresa.

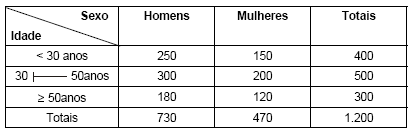
Uma amostra de 2 funcionários será selecionada ao acaso e com reposição dentre esses 1.200. Seja X a variável aleatória que representa o número de funcionários com pelo menos 50 anos. A probabilidade de X ser pelo menos 1 e a média de X são dados, respectivamente, por

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Seja X uma variável aleatória com função densidade de probabilidade dada por:

Utilizando-se o método dos momentos, uma estimativa de β baseada na amostra (0,2; 0,3; 0,5) é dada por

• A.
• B.

  

• C.

  

• D.
• E.

  -1

Certo programa computacional pode ser usado com uma entre três sub-rotinas: A, B e C, dependendo do problema. Sabe-se que a sub-rotina A é usada em 50% das vezes, a B em 30% e a C em 20%. As probabilidades de que o programa chegue a um resultado dentro do limite de tempo são de 80%, caso seja usada a sub-rotina A, 60% caso seja usada a sub-rotina B e 60% caso seja usada a sub-rotina C. Se o programa foi realizado dentro do limite de tempo, a probabilidade de que a sub-rotina A tenha sido a escolhida é igual a

• A.

  

• B.

  

• C.

  

• D.
• E.

  

Seja X a variável aleatória que representa o número de chamadas por minuto recebidas por um PBX. Sabe-se que X tem média λ e que P(X = 3) = P(X = 4). Supondo que a distribuição de Poisson seja adequada para X, a probabilidade de que ocorra uma chamada em 30 segundos é

• A.

  e⁻⁴ .

• B.

  4e⁻⁴ .

• C.

  e⁻² .

• D.

  2e⁻² .

• E.

  1 − 2 e⁻² .

Seja X uma variável aleatória contínua com densidade uniforme no intervalo [-α ,α]. O valor de α que satisfaz à condição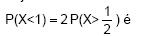

• A.

  1,2.

• B.

  1,5.

• C.

  2,0.

• D.

  2,5.

• E.

  3,0.

Seja X uma variável aleatória contínua com função densidade de probabilidade dada por

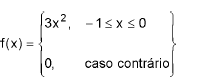
Seja b satisfazendo −1 < b < 0. Então a probabilidade condicional dada por 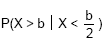 é igual a

• A.

  

• B.
• C.

  

• D.

  

• E.