Questões de Estatística da Fundação Carlos Chagas (FCC)
Lista completa de Questões de Estatística da Fundação Carlos Chagas (FCC) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
A duração de uma lâmpada é uma variável aleatória T, com função densidade de probabilidade (exponencial) dada por
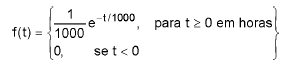
A probabilidade de uma lâmpada durar menos do que 1.200 horas é
- A.
e−1,2
- B.
1 − e−1,2
- C.
- D.
- E.
O seguinte modelo foi ajustado a uma série temporal de produção de certo produto:
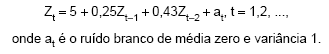
O modelo ajustado
- A.
é um modelo de médias móveis de ordem dois.
- B. é um modelo estacionário, mas com tendência linear.
- C.
tem média 5.
- D.
é um modelo autorregressivo de ordem dois.
- E.
não é invertível.
Três candidatos, A, B e C, disputam as próximas eleições para o Governo do Estado. A, B e C têm respectivamente 30%, 38% e 32% da preferência do eleitorado. Em sendo eleito, a probabilidade de dar prioridade para a Educação é de 30%, 50% e 40%, para os candidatos A, B e C, respectivamente. A probabilidade da Educação não ser priorizada no próximo governo é dada por
- A.
0,446
- B.
0,554
- C.
0,592
- D.
0,644
- E.
0,652
Seja {Xt, t ∈ Z} um processo estocástico onde as variáveis Xt são não correlacionadas, isto é, Cov {Xt, Xs} = 0, t ≠ s e Z é o conjunto dos números inteiros. O processo Xt é um
- A.
passeio aleatório discreto.
- B.
movimento browniano.
- C.
ruído branco discreto.
- D.
processo de Markov.
- E.
processo puramente aleatório.
O custo de realização de um experimento é de R$ 100,00. Se o experimento falhar, haverá um custo adicional de R$ 20,00. Se a probabilidade de sucesso em cada tentativa for 0,3, se as tentativas forem independentes e continuarem até que ocorra o primeiro sucesso, o custo esperado de todo o procedimento é de
- A.
R$ 420,00
- B.
R$ 380,00
- C.
R$ 370,00
- D.
R$ 350,00
- E.
R$ 320,00
Um gráfico de controle de um processo produtivo indica que o processo está sob controle se o conjunto de pontos do gráfico
- A.
tiver todos os pontos situados entre a linha central e o limite superior de controle do gráfico.
- B.
apresentar tendência linear.
- C.
apresentar sazonalidade estocástica.
- D.
apresentar variabilidade crescente ao redor da linha central.
- E.
tiver todos os pontos situados dentro dos limites de controle, tendo um comportamento estacionário.
Seja f(x,y) =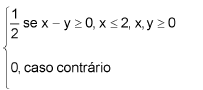 
a função densidade de probabilidade conjunta da variável bidimensional (X, Y). A esperança condicional de Y dado que X = x, denotada por E(Y| x), é igual a
- A.
2/x
- B.
1/x
- C.
2x/3
- D.
x/2
- E.
3x/2
Considere o modelo autorregressivo de ordem dois AR(2) dado por:
Zt = φ1Zt−1 + φ2Zt−2 + at
Onde t a é o ruído branco de média zero e variância 2a σa2 . Se Zt é estacionário, então o valor da função de autocorrelação no lag 1 é
- A.
- B.
- C.
- D.
- E.
Sejam f(k), k = 1,2,3,... e g(k), k = 1,2.3,... as funções de autocorrelação (fac) e autocorrelação parcial (facp), respectivamente, de um modelo ARMA(p,q). Considere as seguintes afirmações:
I. Para um ARMA(1,0), f(k) só difere de zero para k = 1 e g(k) decai exponencialmente.
II. Para um ARMA(1,1), f(k) só difere de zero para k = 1 e g(k) decai exponencialmente.
III. Para um ARMA(0,2), f(k) só difere de zero para k = 1 e k = 2 e g(k) é dominada por misturas de exponenciais ou senoides amortecidas.
IV. Para um ARMA(2,0), f(k) é dominada por misturas de exponenciais ou senoides amortecidas e g(k) = 0, somente para k = 1 e para k > 1 decai exponencialmente.
Está correto o que se afirma SOMENTE em
- A.
I e III.
- B.
III e IV.
- C.
I, II e III.
- D.
III.
- E.
I.
Considere o modelo ARIMA(0,0,2) dado por
Xt = θ0 + at − θ1at−1 + θ2at−2 ,
onde at é o ruído branco de média zero e variância σ2 , e θ0 é uma constante. É correto:
- A.
Xt só é estacionário se
- B.
Xt é um processo sempre invertível.
- C.
Xt só estacionário se
for zero. - D.
Xt é sempre estacionário.
- E.
Xt só é invertível se
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
