Questões de Estatística da Fundação Carlos Chagas (FCC)

Para responder às questões de números 53 a 56, considere as informações da tabela abaixo, que mostra a distribuição de freqüências dos salários mensais dos 50 empregados da Companhia Rancharia.

A média aritmética dessa distribuição, considerando os valores incluídos num determinado intervalo de classe como coincidentes com o ponto médio deste intervalo, é

• A. R$ 2.000,00
• B. R$ 2.500,00
• C. R$ 2.800,00
• D. R$ 3.000,00
• E. R$ 3.200,00

Num período de onze meses, uma empresa vendeu as seguintes quantidades de seu produto: 8, 4, 6, 14, 20, 16, 10, 23, 10, 16, 16. A moda e a mediana foram, respectivamente, iguais a

• A.

  13 e 15

• B.

  13 e 16

• C.

  14 e 13

• D.

  16 e 13

• E.

  16 e 14

Uma pesquisa pretende estimar o valor médio mensal dos salários recebidos pelos professores de 4 escolas do bairro da Saúde. Para a pesquisa primeiramente foram listados todos os professores das 4 escolas segundo o sexo resultando em 2000 professores do sexo feminino e 1 500 professores do sexo masculino. Foram propostos dois planos amostrais distintos. O primeiro plano previa um sorteio com reposição de 350 professores do total de 3500. Na segunda proposta, o total da população de professores seria dividido em dois grupos (um grupo do sexo feminino e outro grupo do sexo masculino) e seriam sorteados 10% de cada grupo com reposição. Segundo a teoria geral da amostragem, o primeiro e o segundo plano são, respectivamente,

• A. Amostragem Aleatória simples e Amostragem estratificada.
• B. Amostragem Aleatória simples e Amostragem sistemática.
• C. Amostragem estratificada e Amostragem aleatória simples.
• D. Amostragem Aleatória simples e Amostragem por conglomerado em dois estágios.
• E. Amostragem Aleatória simples e Amostragem por conglomerados.

• A.

  R$ 1.825,00

• B.

  R$ 1.805,00

• C.

  R$ 1.710,00

• D.

  R$ 1.695,00

• E.

  R$ 1.650,00

Para resolver as questões de números 31 a 33, utilize, dentre as informações dadas a seguir, as que julgar apropriadas.

Se Z tem distribuição normal padrão, então:

P (Z > 2) = 0,023, P (Z < 1,64) = 0,945,

P (0 < Z < 1,5) = 0,433, P (Z < 1,34) = 0,91

Uma corretora de ações, que opera numa certa Bolsa de Valores, faz aplicações financeiras de compra e venda de ações nas áreas Industrial e Comercial, e faz uso de um modelo de probabilidades para a avaliação de seus lucros. O modelo que representa o lucro diário da corretora (em milhares de reais) é dado por:

L = 2 L_I + 3 L_C,

onde

L_I = lucro diário da área Industrial tem distribuição normal com média 5 e variância 16,

L_C = lucro diário da área Comercial tem distribuição normal com média 4 e variância 4.

Supondo independência entre as duas variáveis que compõem L, a probabilidade de um lucro diário superior a 37 mil é

• A. 6,7%
• B. 7,3%
• C. 8,1%
• D. 9,5%
• E. 12,4%

A temperatura T de destilação do petróleo é uma variável aleatória com distribuição uniforme no intervalo [150, 300]. Seja C o custo para se produzir um galão de petróleo. Determine o lucro esperado por galão, supondo que o preço de venda por galão é uma variável aleatória Y dada por: 

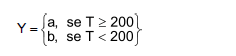
• A. (a + 2b) / 3 − C
• B. (a − C) / 150 + (b − C) / 50
• C. (a + b) / 3 − C
• D. (a + b) / 150 − C
• E. (2a + b) / 3 − C

Seja X uma variável aleatória com função densidade de probabilidade dada por:

• A. e^–4
• B. e^–2
• C. e^–1
• D. e^–1/2
• E. 1

Na transmissão de informação digital, a probabilidade de um bit recebido é classificado como aceitável, suspeito ou inaceitável, dependendo da qualidade do sinal recebido, com probabilidades iguais a 0,8; 0,10 e 0,10, respectivamente. Suponha que as classificações de cada bit sejam independentes. Nos quatro primeiros bits recebidos, seja X o número de bits aceitáveis e Y o número de bits suspeitos. Então P (X = 2, Y = 1) é dada por

• A. 0,00256
• B. 0,00384
• C. 0,00512
• D. 0,0064
• E. 0,0768

Sabe-se que a variável aleatória X é bi-modal para x = 1 e x = 2 e que tem distribuição de Poisson. Sabendo que X é diferente de zero, a probabilidade de X assumir um valor menor do que 3 é dada por

• A.
• B.
• C.
• D.
• E.

Uma pesquisa foi realizada para avaliar se o preço médio do quilo da carne bovina, tipo Alcatra, vendida nos supermercados de dois bairros é igual. No bairro X foram coletados os preços de 15 supermercados e o preço médio obtido foi μ1 com variância 2X S e no bairro Y foram coletados preços de 15 supermercados com preço médio de μ2 com variância 2Y S . Considerando que as distribuições dos preços apresentam distribuição normal e as variâncias populacionais dos dois grupos são iguais e desconhecidas, a distribuição de probabilidade da estatística apropriada para se comparar a média dos dois bairros é

• A. Qui quadrado com 29 graus de liberdade.
• B. F de Snedecor com 3 e 28 graus de liberdade.
• C. t de Student com 30 graus de liberdade.
• D. Normal com média μ1 − μ2.
• E. t de Student com 28 graus de liberdade.