Questões de Estatística da Fundação Carlos Chagas (FCC)

Três métodos de ensino diferentes foram aplicados em três grupos distintos de 6 crianças respectivamente. Após o período de aprendizagem experimental foram aplicados testes, e as médias das notas foram utilizadas para avaliar se existe diferença entre os três métodos de ensino. O pesquisador utilizou a técnica de análise de variância para avaliar a diferença entre as médias dos 3 grupos de alunos. Sabendo que o valor da soma de quadrados entre os grupos foi 70, dentro dos grupos foi 1500 e que o valor crítico da distribuição F (com 5% de significância e 2 e 15 graus de liberdade) para este teste foi 3,68, o valor calculado da estatística F e a decisão do teste são

• A. 0,35 e não existe diferença entre as médias.
• B. 1,85 e a média dos três grupos são iguais.
• C. 0,65 e existe pelo menos um grupo com média diferente.
• D. 0,20 e não existe diferença entre as médias.
• E. 4,00 e não existe diferença entre a média dos grupos.

Em uma população de 100 elementos, com variância populacional 50, foram tomadas amostras casuais simples de tamanho 10. Nestas condições, as variâncias da média amostral na amostragem, com e sem reposição, são respectivamente

• A. 1/5 e 90/99
• B. 2 e 90/99
• C. 4 e 450/99
• D. 5 e 200/99
• E. 5 e 450/99

Em um estudo sobre as vendas dos produtos A, B e C os compradores foram divididos em três categorias de idade (adultos jovens, de 18 a 25 anos; meia idade, entre 36 e 55 anos e idosos, a partir de 56 anos) conforme a tabela a seguir:

O fabricante deseja ter um panorama destas vendas de modo a conseguir ver qualquer destes três produtos e perceber suas associações com os três grupos de idade. Uma técnica de análise multivariada apropriada para este problema é a

• A.

  regressão múltipla.

• B.

  análise de correspondência.

• C.

  regressão logística.

• D.

  análise de variância multivariada.

• E.

  análise de covariância multivariada.

Para responder às questões de números 53 a 56, considere as informações da tabela abaixo, que mostra a distribuição de freqüências dos salários mensais dos 50 empregados da Companhia Rancharia.

Considere a fórmula de Czuber abaixo.

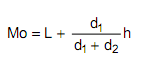
em que:

Mo = moda

L = limite inferior da classe modal

d₁ = diferença entre a freqüência da classe modal e a imediatamente anterior

d₂ = diferença entre a freqüência da classe modal e a imediatamente posterior

h = amplitude do intervalo de classe modal

Desprezando os centavos, o valor da moda dessa distribuição é

• A. R$ 2.666,00
• B. R$ 2.655,00
• C. R$ 2.600,00
• D. R$ 2.566,00
• E. R$ 2.466,00

O histograma de freqüências absolutas a seguir demonstra a distribuição dos salários dos empregados de uma empresa em dezembro de 2006:

Sabendo-se que todos os intervalos de classe referentes a este histograma são fechados à esquerda e abertos à direita, calculou-se a média aritmética dos salários dos empregados, considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo. A moda de Pearson é igual a

• A. R$ 3.000,00
• B. R$ 2.950,00
• C. R$ 2.900,00
• D. R$ 2.850,00
• E. R$ 2.800,00

Para responder às questões de números 21 e 22, considere as informações da tabela abaixo, que mostra a distribuição de freqüência dos salários mensais dos 200 empregados da Companhia XYZ.

Com relação a essa distribuição, é correto afirmar que

• A.

  a média aritmética dos salários é inferior a R$ 700,00.

• B.

  10% dos empregados ganham acima de R$ 1.100,00.

• C.

  mais de 50% dos empregados ganham acima de R$ 900,00.

• D.

  20% dos empregados ganham abaixo de R$ 500,00.

• E.

  35% dos empregados ganham menos de R$ 700,00.

Para responder às questões de números 59 e 60, considere o enunciado a seguir.

O modelo ARIMA(0,0,1) é dado por X_t = θ₀ + a_t − θa_t−1 , onde t a é o ruído branco de média zero e variância σ2 , e θ₀ é uma constante.

Pode-se afirmar corretamente que

• A. X_t só é estacionário se |θ |< 1.
• B. a variância de X_t é dada por θ² .
• C. a variância de X_t é igual a 1.
• D. E(X_t X_t–1) = 1.
• E. X_t é sempre estacionário.

Suponha que uma série temporal sofra uma intervenção. Na sua manifestação essa intervenção pode ser de dois tipos:

• A.

  abrupta ou residual.

• B.

  estacionária ou temporária.

• C.

  integrada ou permanente.

• D.

  estacionária ou não estacionária.

• E.

  linear ou quadrática.

• A. 60
• B. 80
• C. 120
• D. 160
• E. 200

O número de unidades vendidas de um produto por uma empresa apresentou, por meio de um estudo realizado, uma tendência linear de crescimento ao longo do tempo com sazonalidade. A equação da reta de tendência obtida foi Yt = 10 + 50t, em que Yt é o número de unidades vendidas em t, que representa o trimestre correspondente das vendas (t = 1 corresponde ao primeiro trimestre de 2001, t = 2 corresponde ao segundo trimestre de 2001, e assim sucessivamente). Verificando que os movimentos apresentados estavam associados ao nível de tendência, a empresa optou por utilizar o modelo multiplicativo para apurar sua previsão de vendas, usando os fatores sazonais abaixo:

A previsão de vendas, em unidades, para o segundo trimestre de 2007 é

• A. 1.332
• B. 1.392
• C. 1.452
• D. 1.512
• E. 1.572