Questões de Estatística da Fundação Carlos Chagas (FCC)

Instruções: Para responder às questões de números 55 a 57, considere as tabelas a seguir.

Elas fornecem alguns valores da função de distribuição F(x). A tabela 1 refere-se à variável normal padrão, as tabelas 2 e 3 referem-se à variável t de Student com 15 e 16 graus de liberdade, respectivamente:

Supondo-se que a porcentagem da receita investida em educação, dos 600 municípios de uma região, tem distribuição normal com média μ, deseja-se estimar essa média. Para tanto se sorteou dentre esses 600, aleatoriamente e com reposição, 16 municípios e se observou os percentuais investidos por eles em educação. Os resultados indicaram uma média amostral de 8% e desvio padrão amostral igual a 2%. Um intervalo de confiança para μ, com coeficiente de confiança de 96%, é dado por

• A.
• B.
• C.
• D.
• E.

Para a variável aleatória X, observou-se uma amostra aleatória de 6 elementos, a saber: 62, 63, 66, 70, 71 e 72. Considerando-se [63,71] um intervalo de confiança para a mediana de X, esse intervalo tem coeficiente de confiança dado, aproximadamente, por:

• A. 0,97
• B. 0,95
• C. 0,88
• D. 0,78
• E. 0,72

A média aritmética dos salários dos 100 empregados em uma empresa é de R$ 1 500,00. Na hipótese de serem demitidos 20 empregados, que ganham cada um o salário de R$ 2 500,00, e ser concedido, posteriormente, um aumento de 10% em todos os salários dos remanescentes, a nova média aritmética dos salários será de

• A. R$ 1 375,00
• B. R$ 1 350,00
• C. R$ 1 345,00
• D. R$ 1 320,00
• E. R$ 1 300,00

Em uma pesquisa de mercado foi estimado que 50% das pessoas entrevistadas preferem a marca X de um produto. Se, com base no resultado dessa pesquisa, quisermos fazer outra para estimar novamente esta preferência, o tamanho de amostra aleatória simples necessário, para que tenhamos um erro amostral de 0,02 com probabilidade de 95%, deverá ser

• A. 1000
• B. 1024
• C. 2500
• D. 1900
• E. 2000

• A. 162,0 cm
• B. 164,6 cm
• C. 164,8 cm
• D. 166,4 cm
• E. 168,2 cm

Instruções:      Para resolver as questões de números 49 e 50, considere a tabela a seguir, que dá valores das probabilidades P (Z t z) para a distribuição normal padrão.

Os valores de determinado título no mercado de investimentos apresentam uma distribuição considerada normal. Sabe-se que os valores de 16% dos títulos são superiores ou iguais a R$ 10 000,00 e que os valores de 60% dos títulos são inferiores a R$ 7 000,00. A média dos valores destes títulos é

• A. R$ 8 500,00
• B. R$ 8 000,00
• C. R$ 7 500,00
• D. R$ 6 000,00
• E. R$ 4 500,00

Considere a tabela a seguir.

A tabela acima apresenta a distribuição de freqüências relativas do valor do salário pago aos funcionários da fábrica Y no mês de abril de 2006. A média e a mediana do valor do salário pago pela fábrica Y no mês de abril de 2006 são, respectivamente,

• A. R$ 200,00 e R$ 400,00
• B. R$ 900,00 e R$ 1000,00
• C. R$ 1050,00 e R$ 1000,00
• D. R$ 800,00 e R$ 800,00
• E. R$ 900,00 e R$ 900,00

Uma empresa tem 1.000 empregados, classificados conforme a tabela abaixo:

Observação: Calculou-se as médias aritméticas correspondentes para cada grupo e a geral considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo. Para o cálculo das medianas utilizou-se o método da interpolação linear.

Analisando os valores obtidos com relação aos empregados desta empresa, tem-se que

• a.

  a média aritmética e a mediana dos salários dos homens são iguais a R$ 3.250,00 e R$ 3.000,00, respectivamente.

• b.

  a média aritmética e a mediana dos salários das mulheres são iguais a R$ 3.200,00 e R$ 3.000,00, respectivamente.

• c.

  o valor encontrado para a média aritmética dos salários dos empregados de toda a empresa é igual a R$ 3.125,00.

• d.

  o módulo da diferença entre as médias aritméticas dos salários dos 2 grupos é igual a R$ 150,00.

• e.

  o módulo da diferença entre os valores das medianas dos salários entre os 2 grupos é inferior a R$ 150,00.

Uma administradora de imóveis realizou um estudo sobre todos os imóveis alugados em duas regiões, A e B, levantando o seguinte quadro:

Observação: Dada uma seqüência de números, o coeficiente de variação é definido como sendo o quociente da divisão do desvio padrão desta seqüência pela respectiva média aritmética (diferente de zero).

A variância conjunta de A e B, isto é, a variância dos valores dos aluguéis das regiões A e B reunidas é, em (R$)², igual a

• a.

  20.000,00

• b.

  25.000,00

• c.

  32.500,00

• d.

  40.000,00

• e.

  62.500,00

O histograma de freqüências absolutas abaixo demonstra o comportamento dos salários dos 160 empregados de uma empresa em dezembro de 2005:

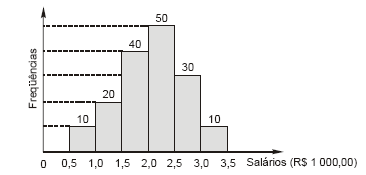
Utilizando as informações nele contidas, calculou-se a média aritmética dos valores dos salários destes empregados, considerando que todos os valores incluídos num certo intervalo de classe são coincidentes com o ponto médio deste intervalo. Escolhendo aleatoriamente um empregado da empresa, a probabilidade dele pertencer ao mesmo intervalo de classe do histograma ao qual pertence a média aritmética calculada é

• A.

  6,25%

• B.

  12,50%

• C.

  18,75%

• D.

  31,25%

• E.

  32,00%