Questões de Matemática
Lista completa de Questões de Matemática para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
- A. 12.000
- B. 14.400
- C. 15.000
- D. 22.500
- E. 36.000
Sejam w = 3 - 2i e y = m +pi dois números complexos, tais que m e p são números reais e i, a unidade imaginária. Se w + y = -1 + 3i, conclui-se que m e p são, respectivamente, iguais a
- A.
-4 e +1
- B.
-4 e +5
- C.
+2 e +1
- D.
+2 e +5
- E.
+4 e -1
Dois números racionais não nulos são inversos entre si quando o produto entre eles resulta no elemento neutro da multiplicação, ou seja, resulta 1. Assim, por exemplo, 0,8 e 1,25 são inversos entre si, pois 0,8 × 1,25 = 1,0. Existe um número real que quando adicionado ao numerador e subtraído do denominador da fração 7 /13 faz com que ela se converta em sua inversa. Esse número é
- A.
um quadrado perfeito, como 4, por exemplo, que é o quadrado de 2.
- B.
primo, ou seja, só é divisível por 1 e por si mesmo.
- C.
decimal não exato, como 1,2 ou 3,51, por exemplo.
- D.
um dos divisores de 24, como 2 ou 3, por exemplo.
- E.
inteiro negativo, como −5, por exemplo.
Considere os números a seguir. Em I e II, o último algarismo repete-se infinitamente. Em III, o padrão de formação da parte decimal repete-se infinitamente.
I) 12,0310540000000000...
II) 12,092740333333333...
III) 12,03003000300003000003...
Acerca desses números, assinale a opção correta.
- A.
Apenas os números I e II são racionais.
- B.
Apenas os números II e III são racionais.
- C.
Apenas o número I é racional.
- D.
Apenas o número III é racional.
- A. I.
- B. II.
- C. III.
- D. I e II.
- E. II e III.
Quantos copos com 200 mL de água, no mínimo, são necessários para encher completamente o vasilhame cônico representado na figura?
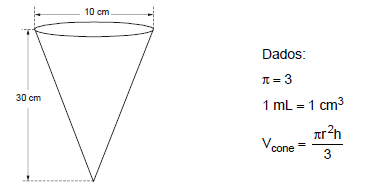
- A.
4 copos.
- B.
5 copos.
- C.
12 copos.
- D.
15 copos.
- E.
16 copos.
Dentre os números complexos abaixo, aquele cujo módulo é igual ao dobro do módulo de z = 4 + 6i é
- A. 3 + 17 i
- B. 8 - 6i
- C.
- D.
- E.
O denominado problema das sete pontes de Königsberg foi resolvido, em 1735, pelo matemático suíço Leonard Euler, a partir de uma forma de modelagem criada por ele e que deu origem à teoria dos grafos. Os grafos são estruturas compostas de dois conjuntos finitos, sendo os elementos de um deles chamados vértices e os elementos do outro pares de vértices chamados arestas. Em termos gráficos, os vértices são como pontos em um plano e as arestas, ligações entre esses pontos. Atualmente, certas informações dificilmente estariam disponíveis sem o uso de grafos, como, por exemplo, as informações sobre as rotas de uma companhia aérea. O problema das sete pontes de Königsberg consiste em determinar um caminho pelo qual um pedestre, partindo de algum ponto de uma região, consiga percorrer todas as sete pontes sem passar mais de uma vez por qualquer uma delas. Euler mostrou que tal caminho não poderia existir. A figura a seguir ilustra um esquema da região, com as pontes representadas pelos arcos.
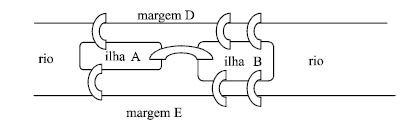
Considerando a figura acima, e identificando os vértices com os pontos em terra e as arestas com as pontes, assinale a opção que representa corretamente o grafo com as mesmas características do problema das sete pontes de Königsberg.
- A.
- B.
- C.
- D.
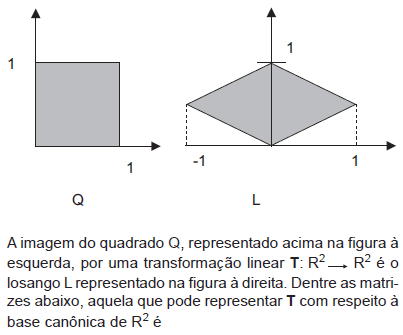
- A.
- B.
- C.
- D.
- E.
Observe a tabela contendo valores de algumas potências de base 3.
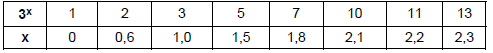
Com base nos valores dessa tabela, qual é a solução da equação 3x = 150?
- A.
4,6.
- B.
4,5.
- C.
4,4.
- D.
4,3.
- E.
4,2.
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
