Questões de Matemática

Considerando que 5 indivíduos tenham idades, em anos, correspondentes aos números inteiros positivos a₁, a₂, a₃, a₄ e a₅, que os números a₁, a₂ e a₅ estejam, nessa ordem, em progressão geométrica com soma igual a 26 e que os números a₁, a₃ e a₄ estejam, nessa ordem, em progressão aritmética de razão 6 e soma igual a 24, julgue os itens a seguir.

A idade do indivíduo mais velho é superior a 20 anos.

• C. Certo
• E. Errado

No caso de duas concorrentes (ABC e XYZ) que apresentam esse quadro de estratégias no contexto da Teoria dos Jogos, verifica-se que, para a empresa ABC,

• A. a estratégia RJ domina a estratégia SP.
• B. a estratégia RJ domina a estratégia MG.
• C. a estratégia SP domina a estratégia MG.
• D. a estratégia MG domina a estratégia SP.
• E. não existe estratégia dominante.

Considerando que 5 indivíduos tenham idades, em anos, correspondentes aos números inteiros positivos a₁, a₂, a₃, a₄ e a₅, que os números a₁, a₂ e a₅ estejam, nessa ordem, em progressão geométrica com soma igual a 26 e que os números a₁, a₃ e a₄ estejam, nessa ordem, em progressão aritmética de razão 6 e soma igual a 24, julgue os itens a seguir.

O indivíduo mais novo tem menos de 3 anos de idade.

• C. Certo
• E. Errado

Existe uma regra prática de divisibilidade por 7 com o seguinte procedimento:

Separa-se o último algarismo da direita. Multiplica-se esse algarismo por 2 e tal resultado é subtraído do número que restou sem o algarismo à direita. Procede-se assim, sucessivamente, até se ficar com um número múltiplo de 7, mesmo que seja zero.

Veja os exemplos a seguir:

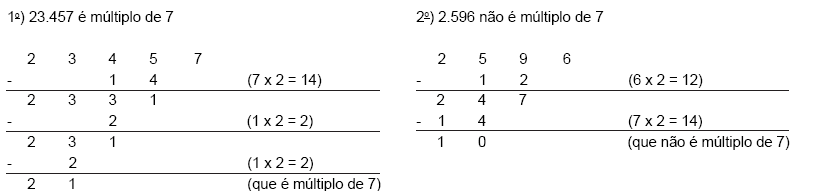
 Seja a um algarismo no número a13.477.307. O valor de a para que este número seja divisível por 7 é

• A.

  1

• B.

  3

• C.

  5

• D.

  7

• E.

  9

Os nove primeiros números ímpares positivos deverão ser distribuídos pelas nove células do quadrado abaixo, de forma que a soma dos números de qualquer linha, qualquer coluna e qualquer diagonal seja sempre S (em cada célula deverá ser colocado um número diferente).

Nessas condições, o número que será colocado na célula escura e o valor de S são, respectivamente,

• A. 5 e 15
• B. 9 e 15
• C. 5 e 27
• D. 9 e 27
• E. 15 e 33

A loja "Tudo Vende" na promoção de venda de um produto cujo custo unitário é de R$ 5,75 se lê: "Leve 3, pague 2" . Usando as condições da promoção, a economia máxima que poderá ser feita na compra de 188 itens desse produto é de:

• A.

  R$ 336,50

• B.

  R$ 356,50

• C.

  R$ 366,50

• D.

  R$ 348,50

No caso das duas concorrentes (ABC e XYZ), adotandose o método de eliminação sequencial de estratégias dominadas, básico no contexto da Teoria dos Jogos, concluise que a empresa ABC

• A. ganhará 40% do mercado.
• B. ganhará 20% do mercado.
• C. ganhará 10% do mercado.
• D. continuará com a mesma fatia de mercado.
• E. perderá 10% do mercado.

Considerando que 5 indivíduos tenham idades, em anos, correspondentes aos números inteiros positivos a₁, a₂, a₃, a₄ e a₅, que os números a₁, a₂ e a₅ estejam, nessa ordem, em progressão geométrica com soma igual a 26 e que os números a₁, a₃ e a₄ estejam, nessa ordem, em progressão aritmética de razão 6 e soma igual a 24, julgue os itens a seguir.

A razão da progressão formada pelos números a₁, a₂ e a₅ é um número fracionário não inteiro.

• C. Certo
• E. Errado

Um homem entra numa livraria, compra um livro que custa 20 reais e paga com uma nota de 100 reais. Sem troco, o livreiro vai até a banca de jornais e troca a nota de 100 por 10 notas de 10 reais. O comprador leva o livro e 8 notas de 10 reais. Em seguida, entra o jornaleiro dizendo que a nota de 100 reais é falsa. O livreiro troca a nota falsa por outra de 100, verdadeira. O prejuízo do livreiro, em reais, sem contar o valor do livro, foi

• A.

  200

• B.

  180

• C.

  100

• D.

  80

• E.

  20

Uma rede de seis localidades é composta por dois fornecedores de determinado produto (localidades 1 e 2), dois centros consumidores desse produto (localidades 3 e 4) e duas localidades (5 e 6), onde ocorre apenas transbordo, isto é, passagem do produto, sem retenção. Considere a seguinte notação: Qij = quantidade de produto fluindo da localidade i para a localidade j; Cij = custo de transportar cada unidade desse produto de i para j; Tij = quantidade máxima transportável da localidade i para a j; Pi = quantidade de produto disponível no fornecedor i (se positiva) ou demandada pelo consumidor i (se negativa). No caso das localidades 5 e 6 onde ocorre apenas o transbordo, tem-se Pi = 0. Se o objetivo for determinar o menor custo possível para o fluxo do produto na rede dos fornecedores 1 e 2 para os consumidores 3 e 4, eventualmente passando pelas localidades 5 e 6, devem ser observadas as seguintes restrições para todo i e todo j:

• A.
• B.
• C.
• D.
• E.