Questões de Matemática

Identifique a equação que corresponde a um hiperboloide de uma folha.

• A.

  x² + 3y² + z² = 3

• B.

  3x² + 3y² + 3z² - 2 = 0

• C.

  -3x² - 3y² + z² = 3

• D.

  x² - 3y² + 2z² = 8

• E.

  x² + 2y² - 4z² = 0

Em informática, o bit foi criado como um padrão conveniente, para representar a diversidade presente em um conjunto que inclui apenas duas mensagens igualmente prováveis, que podem ser identificadas a partir de uma única pergunta do tipo “sim ou não”. Assim, em um grupo formado por duas mensagens, A e B, que têm as mesmas chances de ocorrência, para identificar qualquer uma delas, escolhida ao acaso, basta uma única pergunta do tipo “sim ou não”; em consequência, diz-se que cada uma delas tem uma quantidade de informação igual a 1 bit. Já em um conjunto mais variado, formado, por exemplo, por 4 mensagens equiprováveis A, B, C, D, é possível identificar uma mensagem escolhida ao acaso, com base em duas perguntas do tipo “sim ou não”. Basta separar o conjunto em duas metades e identificar, com uma pergunta, a parte em que se encontra a mensagem escolhida; recorrendo-se a outra pergunta do mesmo tipo, será possível descobrir exatamente a mensagem referida. Nesse caso, diz-se que cada uma das mensagens tem 2 bits de informação. Raciocinando-se de modo semelhante, conclui-se que, em um repertório de 8 mensagens, a quantidade de informação de cada uma delas é igual a 3 bits; se forem 16 as mensagens equiprováveis, cada uma terá 4 bits, e assim por diante.

Embora o número n de mensagens não seja, necessariamente, igual a uma potência inteira de 2, ainda assim é possível medir a quantidade k de informação, em bits, procurando-se o número k tal que

• A.

  k = 2n.

• B.

  2^k = n.

• C.

  k = 2n + 1.

• D.

  2ⁿ = k.

No âmbito da programação linear, minimizar

• A.

  minimizar z’ = (2001.x₁+2010.x10)/₂ , com z’=z

• B.

  minimizar z’ = -2001.x₁+2002.x₂-2003.x₃+...+2010.x10 , com z’=-z

• C.

  maximizar z’ = -2001.x₁-2002.x₂-2003.x₃-...-2010.x₁₀ , com z’=-z

• D.

  maximizar z’ = (2001.x₁+2010.x₁₀)/2 , com z’=z

• E.

  maximizar z’ = +2001.x₁-2002.x₂+2003.x₃-...-2010.x₁₀ , com z’=2.z

Nove caixotes de formato cúbico de 80 cm de aresta foram empilhados conforme representado no desenho.

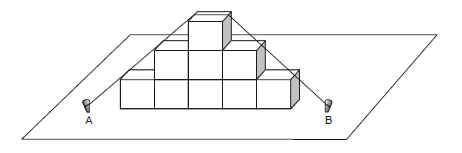
Se a distância entre as estacas A e B é igual a 720 cm, qual é a medida do comprimento da corda esticada entre as estacas para manter o arranjo fixo?

• A.

  880 cm.

• B.

  800 cm.

• C.

  780 cm.

• D.

  720 cm.

• E.

  680 cm.

O valor máximo da função de variável real 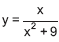 é

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

No desenho abaixo podemos observar uma circunferência sobre a qual foram assinalados 4 pontos (A, B, C e D). De um ponto P, externo à circunferência, foram traçadas duas semi retas, uma delas passando por C e D e a outra por A e B. Nessa situação, ficaram formados dois triângulos semelhantes: PBC e PDA.

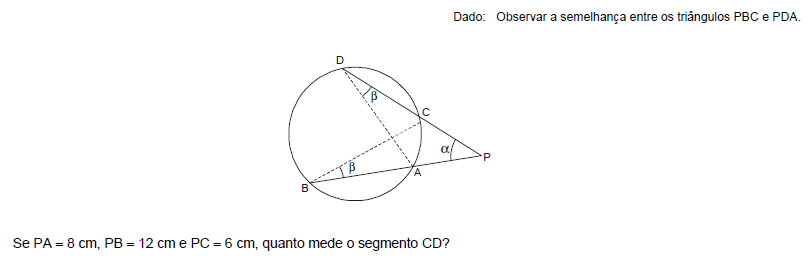
• A.

  8 cm.

• B.

  10 cm.

• C.

  11 cm.

• D.

  12 cm.

• E.

  14 cm.

O gráfico abaixo mostra a curva de custo total médio de uma empresa, em função da quantidade produzida.

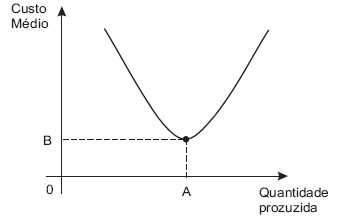
Considerando o gráfico, afirma-se que o(a)

• A.

  custo variável de produção é nulo.

• B.

  custo fixo de produção é necessariamente nulo.

• C. custo total diminui com o aumento da produção até A.
• D.

  empresa deve produzir a quantidade A para maximizar seu lucro.

• E.

  curva de custo marginal passa pelo ponto de coordenadas (A, B).

• A.
• B.
• C.
• D.
• E.

Em certo ano, determinada cooperativa conseguiu vender a caixa de laranja ao preço de R$ 6,00 na safra e de R$ 13,00 na entressafra, tendo arrecadado um total de R$ 880.000,00 pela venda de 100 mil dessas caixas. Nesse caso, denominando-se por x e y, respectivamente, as quantidades de caixas vendidas pela cooperativa na safra e na entressafra, as equações que modelam adequadamente a situação descrita são x + y = 100.000 e

• A.

  6y +13x = 880.000.

• B.

  6x +13y = 880.

• C.

  6x +13y = 880.000.

• D.

  6y +13x = 880.

Considere a figura seguinte:

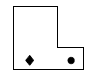
Se fosse possível deslizar tal figura sobre a folha em que ela está desenhada, certamente ela coincidiria com a figura:

• A.

  

• B.

  

• C.

  

• D.

  

• E.