Questões de Matemática do ano 2006

De uma peça quadrada de madeira de 2,2m de lado, um marceneiro recortou um tampo de mesa perfeitamente redondo, com o maior diâmetro possível. Qual a área aproximada, em m^2, desse tampo de madeira?

• A.

  15,2

• B.

  13,8

• C.

  9,6

• D.

  6,9

• E.

  3,8

Considere a figura abaixo:

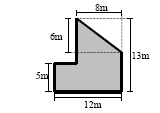
A área da região hachureada é de:

• A.

  60 m²

• B.

  84 m²

• C.

  92 m²

• D.

  100 m²

• E.

  156 m²

Um livro de 350 páginas tem 2cm de espessura. Dentre os valores abaixo, o que representa com mais precisão a espessura aproximada de cada página, em milímetros, é:

• A. 0,046
• B. 0,057
• C. 0,066
• D. 0,070
• E. 0,082

Qual é a área de um terreno retangular cuja medida frontal é de 30 metros e a diagonal é de 50 metros?

• A.

  1500m².

• B.

  1400m².

• C.

  1200m².

• D.

  1300m²

Uma peça de lona retangular tem 10m de comprimento e 1,2m de largura. Qual é o número máximo de pedaços quadrados, de 0,25m2 de área, que podem ser cortados dessa peça?

• A.

  48

• B.

  44

• C.

  40

• D.

  30

• E.

  20

Uma mesa quadrada tem 2.500 cm2 de área. Em quanto tempo um ratinho adestrado, andando a uma velocidade de 5cm/s, contornará essa mesa?

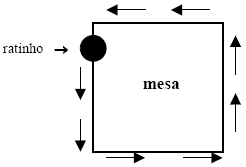
• A.

  10 segundos.

• B.

  20 segundos.

• C.

  25 segundos.

• D.

  30 segundos.

• E.

  40 segundos.

Uma caixa apresenta as seguintes medidas: 200 centímetros de comprimento, 40 decímetros de largura e 5.000 milímetros de profundidade. Se aumentarmos em 50% o seu comprimento e diminuirmos em 30% a sua profundidade, qual a razão entre o volume final e o inicial?

• A.

  

• B.
• C.
• D.
• E.

Analise a figura abaixo.

O maior número de triângulos distintos que podem ser vistos nessa figura é

• A.

  20

• B.

  18

• C.

  16

• D.

  14

• E.

  12

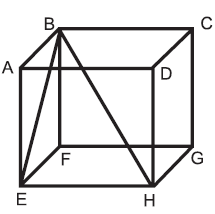
Dado o cubo ABCDEFGH de arestas medindo 1, pode-se afirmar que a distância entre:

• A. um ponto do segmento BE e um ponto do segmento DH é sempre maior que 1.
• B. um ponto do segmento BE e um ponto do segmento BH é sempre maior que 0.
• C. um ponto do segmento CD e um ponto do segmento EF é sempre maior que 1
• D. os pontos G e D é 1.
• E. os pontos A e H é igual à distância entre B e C.

Um auditório, que tem a forma de um triângulo isósceles OPQ, em que o ângulo POQ é reto e a hipotenusa PQ mede  conforme ilustra a figura acima, foi atingido pelo fogo. O incêndio se propaga de modo que sua frente SR avança em linha reta na direção da hipotenusa, como mostrado na figura. Suponha que em x minutos a frente de SR avança x metros em cada cateto da sala e que a área da região ainda não atingida seja expressa pela função  m². Com relação a essa situação hipotética, assinale a opção correta.

• A.

  Se, para determinado x, tem-se que SR = m, então para esse x, f(x) = 184 m².

• B.

  Decorridos 720 segundos, a área da região ainda não atingida pelo fogo é inferior a 130 m².

• C.

  O tempo gasto para queimar 16% do total da área da sala é inferior a 5 minutos.

• D.

  São necessários mais de 25 minutos para queimar toda a sala.