Questões de Matemática do ano 2006

Observe a figura abaixo:

Essa figura mostra um semicírculo de diâmetro AC, no qual foram construídos os semicírculos de diâmetros AB e BC, formando a área da região hachurada. Pode-se afirmar que a medida desta área, em mm², é igual a:

• A.

  

• B.

  

• C.

  

• D.

  

Uma estrutura feita de arame tem a forma de um cubo cujo lado mede 40 cm. Uma formiga encontra-se sobre um vértice do cubo (ponto A), conforme é mostrado na figura abaixo.

Observou-se que: essa formiga saiu do ponto A, foi caminhando ao longo do fio e, após ter percorrido a maior distância possível, retornou ao ponto de partida. Se ela passou uma única vez sobre cada vértice, é correto afirmar que a distância que percorreu, em centímetros, era

• A.

  80

• B.

  160

• C.

  240

• D.

  320

• E.

  400

Analise atentamente as figuras abaixo:

Os números de vezes que as figuras 2, 3 e 4 aparecem no interior da figura 1 são, respectivamente,

• A.

  2, 3 e 3

• B.

  3, 3 e 4

• C.

  4, 3 e 3

• D.

  4, 3 e 4

• E.

  4, 4 e 3

Analise a figura seguinte:

Dos desenhos seguintes, aquele que pode ser encontrado no interior da figura dada é

• A.
• B.
• C.
• D.
• E.

Observe que com 10 moedas iguais é possível construir um triângulo:

Movendo apenas três dessas moedas é possível fazer com que o triângulo acima fique com a posição invertida, ou seja, a base para cima e o vértice oposto para baixo. Para que isso aconteça, as moedas que devem ser movidas são as de números

• A.

  1, 2 e 3

• B.

  1, 8 e 9

• C.

  1, 7, e 10

• D.

  2, 3 e 5

• E.

  5, 7 e 10

A figura seguinte mostra uma pilha de cubos de mesmas dimensões.

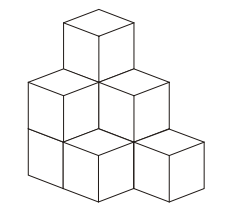
O número de cubos que foram usados na montagem dessa pilha é

 

 

 

• A.

  8

• B.

  9

• C.

  10

• D.

  11

• E.

  12

                              

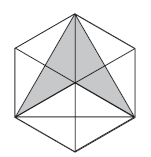
Um hexágono regular foi repartido em duas regiões: uma clara e outra escura. A razão entre as áreas das regiões escura e clara, nessa ordem, vale:

• A.
• B. 1
• C.
• D.
• E.

Um engenheiro avalia se duas paredes em uma edificação estão em ângulo de 135º do seguinte modo: traça dois segmentos OP e OQ de 5cm, um em cada parede, à mesma altura do solo, de modo que o ponto O esteja na aresta comum às paredes.

Mede, então, a distância d de P a Q. Constatando-se que o ângulo era menor do que o desejado, pode-se afirmar que:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

Sabe-se que o número N de habitantes de um município da cidade de Baraúna, cresce em função do tempo t, em anos, de acordo com a expressão N = 5000.(1,2)^t. Em 1998, quando t = 0, a população era de 5 000 habitantes. A população no ano 2001 era, em número de habitantes, igual a

• A. 8640.
• B. 8530.
• C. 7890.
• D. 7230.
• E. 6880.

Certo plano de saúde emite boletos para pagamento bancário com as seguintes condições:

Um conveniado desse plano de saúde pagaria R$ 1.198,00 se tivesse feito o pagamento até o vencimento. Porém, houve alguns dias de atraso, o que acarretou uma multa de 10% e juros de R$ 0,60 por dia de atraso. Como ele pagou um acréscimo de R$ 124,00, o total de dias em atraso foi igual a

• A. 3.
• B. 4.
• C. 5.
• D. 6.
• E. 7.