Questões de Matemática do ano 2006

Um restaurante a quilo vende 200 kg de comida por dia, a R$ 12,00 o quilo. Uma pesquisa de opinião revelou que, para cada aumento de R$ 1,00 no preço, o restaurante perderia 10 fregueses, com um consumo médio de 500 g cada. Para um certo preço, o restaurante pode ter uma receita máxima. Essa receita, em reais, é de:

• A. 4000
• B. 3690
• C. 3380
• D. 3125

Num teatro, quando o preço do ingresso para um espetáculo é P , o número de espectadores que a ele assiste é E. Para cada redução δ no preço do ingresso, há um aumento de espectadores Δ. Para que a receita do espetáculo seja máxima, o ingresso deve ter o seguinte preço:

• A.
• B.
• C.
• D.

Considerem-se as funções quadráticas definidas por y =(a + 1)x² − 2ax −(3a + 7) na variável x, com o parâmetro a. Todos os gráficos destas funções apresentam uma corda comum. O comprimento da corda é:

• A.
• B.
• C.
• D.

Sejam 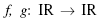 funções ímpares.  Então podemos sempre afirmar que o gráfico de h = f × .g é simétrico com relação ao (à)

• A.

  eixo dos x.

• B.

  eixo dos y.

• C.

  reta y = x.

• D.

  reta y = - x.

• E. origem.

Se h(x) = ( f og)(x) , h(x) x² - 2x +1, g(x) = x +1 e f (x) é uma função quadrática, a soma das raízes de f é

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5

NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.

A função f: A → B, definida por f(x) = x ^3, admite inversa quando seu domínio A e contra domínio B forem:

• A.

  

• B.

  

• C.

  

• D.

  

NAS QUESTÕES NUMERADAS DE 16 A 40, ASSINALE A ÚNICA ALTERNATIVA QUE RESPONDE CORRETAMENTE AO ENUNCIADO.

Quando existe uma bijeção entre os conjuntos A e B, é correto afirmar que:

• A.

  os conjuntos A e B possuem a mesma quantidade de elementos.

• B.

  não é possível estabelecer qualquer comparação entre a quantidade de elementos dos conjuntos A e B.

• C.

  a quantidade de elementos do conjunto A é menor do que a quantidade de elementos do conjunto B.

• D.

  a quantidade de elementos do conjunto B é menor do que a quantidade de elementos do conjunto A.

Uma clínica de fisioterapia oferece três opções de pagamento para os pacientes:

Opção A: uma matrícula de R$ 50,00 e mais R$ 10,00 por sessão de fisioterapia.

Opção B: R$ 15,00 por sessão de fisioterapia, independente do número de sessões do tratamento.

Opção C: um valor fixo de R$ 150,00 para até dez sessões de fisioterapia; as sessões que passarem desse número serão cobradas à razão de R$ 10,00 por sessão.

Nessas condições, podemos afirmar que:

• A.

  para um paciente que precisa de menos de 10 sessões, a Opção A é mais vantajosa.

• B.

  para um paciente que precisa de menos de 10 sessões, a Opção B é mais vantajosa.

• C.

  para um paciente que precisa de menos de 10 sessões, a Opção C é mais vantajosa.

• D.

  para um paciente que precisa exatamente de 10 sessões, a Opção C é mais vantajosa.

• E.

  para um paciente que precisa de mais de 10 sessões, a Opção B é mais vantajosa.

Uma função polinomial do segundo grau () x f tem seus zeros nos pontos 1 = x e 5 = x e coeficiente do termo de maior grau unitário. Nessas condições podemos afirmar que:

• A.

  f (x) = x² − 5x − 6 .

• B.

  f (x) = x² + 6x + 5.

• C.

  f (x) = x² − 5x + 6

• D.

  f (x) é máxima para x = 3 .

• E.

  f (x) é mínima para x = 3 .

Se a função linear f(x) = mx + b satisfaz a condição

f(7x – 2) = 7f(x) – 2,

 pode-se afirmar, corretamente, que

• A.

  m = –3b – 1

• B.

  m = –3b + 1

• C.

  m = 3b – 1

• D.

  m =3b + 1