Questões de Matemática do ano 2007

Um professor deu a seus alunos o seguinte problema para ser resolvido: "Um grupo de pessoas iriam dividir igualmente a quantia de R$ 2000,00. No último momento, decidiram de comum acordo, que 10 pessoas desse grupo não teriam direito a participar dessa divisão. Nesse caso então, cada um dos restantes do grupo acabou recebendo R$ 20,00 a mais. Quantas pessoas participavam inicialmente do grupo?" Assinale o item com a equação que descreve tal situação:

• A.
• B.
• C.
• D.
• E.

Considere o problema abaixo, proposto a alunos de 6ª série do ensino fundamental.

Para resolver esse problema com competência, seus alunos devem ter desenvolvido, entre outras, a habilidade de

• A.

  estabelecer relação de congruência entre retângulos.

• B.

  determinar as medidas dos lados de um quadrado.

• C.

  compor e decompor figuras geométricas.

• D.

  determinar os divisores de um número natural.

• E.

  identificar os múltiplos de um número natural.

Dentre as habilidades que os alunos do 3º ciclo (5ª e 6ª séries) devem desenvolver (PCN-Matemática) salientamos a de utilizar a linguagem algébrica para representar as generalizações inferidas a partir de padrões, tabelas e gráficos em contextos numéricos e geométricos. Para avaliar tal habilidade, um professor propôs a seus alunos o seguinte problema:

Os polígonos que compõem cada figura da seqüência abaixo são triângulos e quadrados.

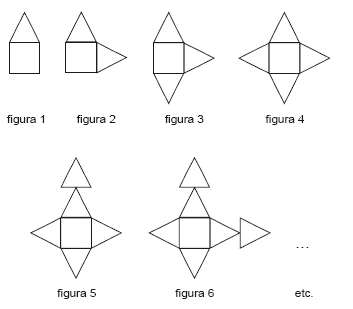
Sabendo como é a figura 10 dessa seqüência, represente o número de triângulos que devem ser acrescentados a ela para se obter a n-ésima figura dessa seqüência, sendo n > 10.

A resposta a essa questão é

• A.

  n

• B.

  n − 10

• C.

  10(n + 10)

• D.

  (n − 10) + (n + 10)

• E.

  (n + 10)²

Com o objetivo de levar seus alunos a

− eleger as operações que resolvem um problema;
− relacionar diferentes registros de números racionais;
− realizar cálculos com números racionais, por processos pessoais ou convencionais;

um professor propôs a seus alunos a seguinte questão:

Os alunos que tinham desenvolvido aquelas habilidades elegeram, acertadamente, a alternativa

• A.

  A

• B.

  B

• C.

  C

• D.

  D

• E.

  E

Segundo os PCN de Matemática, quando o conceito de multiplicação é explorado apenas no campo dos números naturais: o efeito da multiplicação é sempre o de aumentar. Assim, para colocar o aluno frente a situações que o faça questionar tal crença, é possível propor a ele, entre outras, uma situação-problema como:

• A.

  Numa loja de artigos de cama, mesa e banho, foram vendidos somente na quinta-feira 37 toalhas de rosto a R$ 7,80 cada uma. Que quantia essa loja recebeu com essa venda?

• B.

  Se eu tinha R$ 32,50 na carteira e fiz apenas uma compra de R$ 12,30, com quanto fiquei na carteira após essa compra?

• C.

  Paulo se encontra no topo de uma escada, a uma altura de 3,5 m em relação ao solo. Se a altura de cada degrau dessa escada é de 0,20 m, então quantos degraus ela tem?

• D.

  Num depósito vazio, são empilhadas 3 caixas com 30 cm, 45,5 cm e 62 cm de altura, respectivamente. Qual é a altura da pilha formada?

• E.

  Uma padaria tem em seu estoque 20 pacotes de 0,250 kg de fermento. De quantos quilos de fermento essa padaria dispõe no estoque?

Na página 32 do Referencial de expectativas para o desenvolvimento da competência leitora no ciclo II do ensino fundamental − Matemática, é feita uma crítica à quase que exclusiva proposta que se tem observado em sala de aula de que nas situações-problema oferecidas aos alunos, todos os dados devem ser utilizados e combinados para se obter a resposta que, deve ser única. Nessa crítica, esse Referencial propõe que sejam observados outros aspectos nos problemas propostos, apresentando enunciados que forneçam

• A.

  exatamente 3 dados, para serem combinados entre si durante a resolução.

• B.

  dados supérfluos, isto é, mais dados do que os necessários para a resolução do problema.

• C.

  necessariamente dados de outros campos do conhecimento que não aquele em que o contexto do problema está inserido.

• D.

  representações geométricas dos dados apresentados, para sua melhor concretização.

• E.

  apenas dados numéricos, para que os alunos possam calcular com mais competência.

Alguns relógios utilizam a numeração romana no mostrador como referência à tradição. Observando o mostrador de um desses relógios um aluno notou que a escrita do número 9 era VIIII, e não IX, como seu professor havia ensinado. Sobre essa diferença observada por ele, é correto afirmar que

• A.

  a marcação desse relógio, e de todos os relógios semelhantes a esse, está errada.

• B.

  a marcação refere-se ao sistema de numeração romano anterior à utilização do princípio subtrativo.

• C.

  no sistema romano mais moderno de numeração o 9 pode ser escrito das duas formas.

• D.

  ambas as formas de escrita do 9 não estão de acordo com as regras de formação dos números no sistema romano de numeração.

• E.

  o professor cometeu um deslize ao ensinar errado a escrita do 9 no sistema romano de numeração.

Na primeira fase de um concurso, os candidatos foram distribuídos em salas de 40 lugares, sendo que apenas uma delas ficou incompleta, com 25 candidatos. Na segunda fase desse concurso, o número de candidatos diminuiu em 985. Considerando-se que foram usadas ainda salas de 40 lugares, quantos candidatos ficaram em uma sala incompleta?

• A.

  em número de 25 candidatos;

• B.

  não se pode definir o número de candidatos;

• C.

  um candidato;

• D.

  nenhum candidato.

O indicador de combustível do veículo de João marcava 3/10 de sua capacidade total quando parou para abastecer. O frentista colocou 20 litros de combustível e o indicador registrou 7/10. A capacidade total desse tanque, em litros, é de:

• A. 45
• B. 50
• C. 40
• D. 55
• E. 60

Em determinado instante de uma corrida, em que os participantes partiram de um mesmo ponto de saída, os competidores C₁, C₂, C₃ e C₄ estão nas posições P₁, P₂, P₃ e P₄ da pista, respectivamente. Sabendo que se i < j, então a posição P_i está mais próxima do ponto de partida do que P_j, e que P_iP_j é a distância entre os competidores C_i e C _j, para i e j = 1, 2, 3 e 4, julgue os itens a seguir.

Considere que as velocidades dos competidores são constantes, isto é, para cada competidor, a sua velocidade pode ser calculada pelo quociente

Nessa situação, se a velocidade do competidor C₁ for igual  a da velocidade do competidor C₂, então, no instante em que o competidor C₂ estiver na metade do percurso total, a distância entre esses dois competidores será igual  a do percurso total.

• C. Certo
• E. Errado