Questões de Matemática do ano 2008

Se IR denota o conjunto dos números reais e f (x) = 2x + 7 e g(x) = x² − 2x + 3 são funções de IR em IR, então a lei de definição da função composta f o g é dada por

• A.

  x² − 3x +1

• B. 2x² − 4x +13
• C. x⁴ − 3x² + 9
• D. 2x⁴ − 5x² + 36
• E. x⁴ − x² + x −1

Seja f uma função que tem como domínio o conjunto A ={Ana, José,Maria, Paulo, Pedro} e como contradomínio o conjunto B ={1, 2, 3, 4, 5}. A função f associa a cada elemento x em A o número de letras distintas desse elemento x . Com base nessas informações, pode-se afirmar que

• A.

  elementos distintos no domínio estão associados a distintos elementos no contradomínio.

• B.

  todo elemento do contradomínio está associado a algum elemento do domínio.

• C.

  f não é uma função.

• D. f (Maria) = 5 .
• E. f (Pedro) = f (Paulo).

Duas pessoas A e B estão paradas sobre uma mesma estrada reta, e a distância entre elas vale D. Essas pessoas começam a caminhar, ao mesmo tempo, uma em direção à outra. A encontra B depois de percorrer da distância D. É correto, então, concluir que B caminhou

• A. um terço da distância percorrida por A.
• B. a metade da distância percorrida por A.
• C. a mesma distância que A.
• D. o dobro da distância percorrida por A.
• E. o triplo da distância percorrida por A.

Com relação a equações e funções de 1.º e 2.º graus e logaritmos, julgue os itens que se seguem.

No sistema de coordenadas cartesianas xOy, considere uma função de 1.º grau y = f (x) = ax + b, em que a < 0 e b > 0. Considere também que a área da região triangular compreendida entre o gráfico da f e os eixos coordenados seja igual a 54 unidades de área e que a soma dos comprimentos dos dois lados menores desse triângulo seja igual a 24 unidades de comprimento. Nessa situação, existem duas funções de 1.º grau que cumprem as condições enunciadas e para essas duas funções a + b = 15.

• C. Certo
• E. Errado

Um estudante quer saber o quanto ele caminha de sua casa até a escola que freqüenta. O bairro da cidade onde fica a sua casa e a sua escola é divido em quarteirões, quadrados que medem 500 m de lado. Com o objetivo de medir tal percurso, é possível considerar esse bairro em um sistema de coordenadas cartesianas ortogonais xOy, em que o centro O = (0, 0) desse sistema corresponde à casa do estudante. Para isso, como unidade de medida, adota-se o comprimento dos lados dos quarteirões desconsiderado a largura das ruas que, ao formarem os contornos dos quarteirões, são paralelas ou perpendiculares aos eixos coordenados. A direção Norte-Sul corresponde ao eixo das ordenadas (com orientação de Sul para Norte), e a direção Leste- Oeste, ao eixo das abcissas (com orientação de Oeste para Leste). Assim, considerando esse sistema de coordenadas, a escola fica no vértice superior esquerdo do quarteirão que encontra-se a dois quarteirões a Oeste e três quarteirões ao Norte da casa do menino.

Com base nas informações apresentadas, julgue os itens seguintes.

A reta que passa pela escola e é perpendicular à que contém a casa do menino e a escola, tem coeficiente linear igual a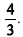

• C. Certo
• E. Errado

Julgue os itens a seguir, acerca de um reservatório de gás que tem a forma de uma esfera de 10 m de raio.

Um reservatório esférico que tem raio igual à metade do raio do reservatório original terá área de superfície igual à metade da área da superfície do reservatório original.

• C. Certo
• E. Errado

Julgue os itens a seguir, acerca de um reservatório de gás que tem a forma de uma esfera de 10 m de raio.

Se for construído um novo reservatório esférico, com raio igual à metade do raio do reservatório original, então o volume desse novo reservatório será igual à metade do volume do outro reservatório.

• C. Certo
• E. Errado

Julgue os itens a seguir, acerca de um reservatório de gás que tem a forma de uma esfera de 10 m de raio.

A área de superfície do reservatório é igual a 400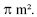

• C. Certo
• E. Errado

Julgue os itens a seguir, acerca de um reservatório de gás que tem a forma de uma esfera de 10 m de raio.

O volume desse reservatório é igual a 4.000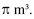

• C. Certo
• E. Errado

Se P = (x₀ , y₀ , z₀ ) for um ponto da esfera de equação x² + y² + z² = 4, então a equação do plano tangente à esfera, nesse ponto P, pode ser escrita como

• A.

  x(x₀ - y₀ ) + y(y₀ - z₀ ) + zz₀ = 4.

• B.

  xx₀ + yy₀ + zz₀ = 4.

• C.

  xx₀ + y(y₀ - z₀ ) + zz₀ = 4.

• D.

  x(x₀  - y₀ ) + yy₀ + zz₀ = 4.