Questões de Matemática do ano 2011
Lista completa de Questões de Matemática do ano 2011 para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
Os números complexos z1, z2 e z3 formam, nessa ordem, uma progressão aritmética e são tais que z1 + z2 + z3 = 6 + 9i, onde i representa a unidade imaginária. Sendo assim, (z2)2 é igual a
- A.
− 5
- B.
− 5 + 6i
- C.
− 5 + 12i
- D.
13 + 6i
- E.
13 + 12i
Seja z = (t 2 4t + 4) + (2t + 8)i. Para que z seja um imaginário puro, o valor de t deve ser:
- A.
-4.
- B.
-2.
- C.
0.
- D.
2.
- E.
4.
- A.
-1 e 0
- B.
-2 e 1
- C.
-3/2 e 1/2
- D.
0 e -1
- E.
1 e -2
- A.
3
- B.
- C.
- D.
- E.
- A.
m + n = 0
- B.
m + n = 4
- C.
m = 3n
- D.
m.n = 8
- E.
m.n = 1
Os vetores não nulos u e v são tais que (u + v) e (u - v) são perpendiculares. Se |u| e |v| são os módulos de u e de v, respectivamente, então,
- A.
|u| . |v| = 1
- B.
|u| . |v| = 0
- C.
|u| + |v| = 0
- D.
|u| |v| = 1
- E.
|u| |v| = 0
- A.
1 e 2
- B.
2 e 3
- C.
3 e 4
- D.
4 e 5
- E.
5 e 6
- A.
0
- B.
1
- C.
log3 60 + log4 60 + log5 60
- D.
log3 60.log4 60 + log4 60.log5 60 + log5 60.log3 60
- E.
- A.
0
- B.
1
- C.
- D.
- E.
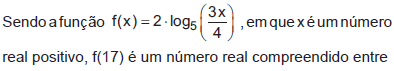
- A.
1 e 2
- B.
2 e 3
- C.
3 e 4
- D.
4 e 5
- E.
5 e 6
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
