Questões de Matemática do ano 2017

Uma das diagonais de um retângulo ABCD representado no plano cartesiano é o segmento AC cujas extremidades A (x – 2;5) e C (2x – 4;9) pertencem ao 1º quadrante. Sendo a abscissa de C maior que a abscissa de A e a área desse retângulo igual a 64, então a soma dos algarismos do número x é:

• A. 5.
• B. 6.
• C. 7.
• D. 8.
• E. 9.

Considere a seguinte tabela:

Considerando que, quando a economia cresce, o desemprego cai e o salário aumenta, o valor de x será igual a:

• A. 960;
• B. 600;
• C. 375
• D. 305;
• E. 120.

na posição inicial P = 0 e a tartaruga, em vantagem, na posição P = d > 0, então Aquiles alcançará a tartaruga na posição

• A. d/2.
• B. d.
• C. 3d/2.
• D. 2d.
• E. 7d/4.

Se T é um número real positivo, então a área da região limitada pelo gráfico da função f referida no texto 11A3CCC, pelo eixo Ox e pela reta vertical x = T será igual a

• A. 50 + 8T, se T  10.
• B. 8T - 30, se T  10.
• C. T ², se 0 T  10.
• D. T ² + 8T, se T 10.
• E.

A derivada, f N(x), da função f apresentada no texto 11A3CCC pode ser calculada para diversos valores x do domínio da f. Dessa forma, f N(x) será expressa por

• A. f '(x) = 1, para 0 < x < 10; e f N(x) = 0, para x >10.
• B. f 1(x) = 1, para 0 < x < 10; e f N(x) = 0, para $10.
• C. f '(x) = 1, para 0 x 10; e f N(x) = 0, para x >10.
• D. f '(x) = 1, para 0  x 10; e f N(x) = 0, para x $10.
• E. f '(x) = 1, para 0 # x < 10; e f N(x) = 0, para  $10.

Ainda com referência ao texto 11A3CCC, a função f

• A. possui uma única descontinuidade e essa descontinuidade é do tipo salto.
• B. possui uma única descontinuidade e essa descontinuidade é do tipo removível.
• C. é uma função contínua em todos os pontos de seu domínio.
• D. é uma função descontínua em mais de um ponto de seu domínio.
• E. possui uma única descontinuidade e essa descontinuidade é do tipo infinito.

Na situação apresentada no texto 11A3CCC, se os valores de x forem superiores a 9 e se aproximarem de 10 por valores menores que 10, então os valores de f(x)

• A. tenderão ao infinito.
• B. se aproximarão de 8.
• C. se aproximarão de 9.
• D. se aproximarão de 10.
• E. oscilarão entre 8 e 10.

Considerando que f(x) e g(x) sejam as funções definidas no texto 11A1AAA, assinale a opção correta a respeito do sinal da função 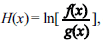que está definida para todo x do intervalo (0, 720), em que ln[x] é o logaritmo natural de x.

• A. H(x) 0 para todo x do intervalo (0, 720).
• B. H(x) 0 para todo x do intervalo (0, 1) e H(x) > 0 para todo x do intervalo (1, 720).
• C. H(x)  0 para todo x do intervalo (0, 360] e H(x) < 0 para todo x do intervalo (360, 720).
• D. H(x)  0 para todo x do intervalo (0, 360] e H(x) > 0 para todo x do intervalo (360, 720).
• E. H(x) 0 para todo x do intervalo (0, 720).

Ainda considerando as funções f(x) e g(x) definidas no texto 11A1AAA, se x é tal que

• A. x > 450.
• B. x < 270.
• C. 270 x < 330.
• D. 330  x 390.
• E. 390 < x450.

Ainda com base no texto 11A1AAA, se m(x) = x - 240, e se a função composta Q(x) = (gBm)(x) = g(m(x)) representa a quantidade de litros de combustível que resta no tanque de um veículo depois de percorrer x quilômetros, tendo iniciado o percurso com o tanque cheio, então o tanque de combustível desse veículo tem capacidade para

• A. mais de 90 litros e menos de 95 litros.
• B. mais de 95 litros.
• C. 80 litros.
• D. mais de 80 litros e menos de 85 litros.
• E. mais de 85 litros e menos de 90 litros.