Questões sobre Funções

O conjunto que descreve o domínio máximo da função a valores reais dada por  é o subconjunto dos números reais satisfazendo a propriedade:

• A.

  −1≤ x ≤1 ou x ≥ 10

• B.

  −1≤ x ≤1 e x ≥ 10

• C.

  x ≤ − 1 ou x ≥10

• D.

  x ≤ − 1 e x ≥10

• E. x ≤ − 1 ou x ≥10 ou x ≥1

Considere a função tendo como domínio e contradomínio o conjunto dos números reais definida por f(x)=4^|x| e as seguintes afirmações sobre a mesma:

I- A função f é estritamente crescente ,

II- A função f possui inversa

III- O gráfico de f não corta o eixo x.

IV- O número real 2 pertence ao conjunto imagem de f.

São verdadeiras as afirmações:

• A.

  I e II

• B.

  II e III

• C.

  I e III

• D.

  III e IV

• E.

  II e IV

Considere que a produção de óleo cru, em milhares de barris por dia, de uma bacia petrolífera possa ser descrita por uma função da forma 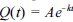, em que A e k são constantes positivas, t é o tempo, em anos, a partir do ano t = 0, que corresponde ao ano de maior produtividade da bacia. Com base nessas informações, julgue os itens a seguir.

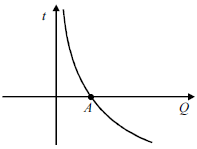
Considerando a função Q(t) referida no texto como definida para todo t real, é correto afirmar que o gráfico de sua inversa, t = t(Q), tem o aspecto indicado na figura abaixo.

• C. Certo
• E. Errado

Considere que a produção de óleo cru, em milhares de barris por dia, de uma bacia petrolífera possa ser descrita por uma função da forma 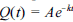, em que A e k são constantes positivas, t é o tempo, em anos, a partir do ano t = 0, que corresponde ao ano de maior produtividade da bacia. Com base nessas informações, julgue os itens a seguir.

Considere que a maior produtividade da bacia tenha sido de 1.200.000 barris de óleo cru por dia e, 10 anos depois, a produtividade caiu para 800.000 barris por dia. Nessa situação, depois de 20 anos, a produção caiu para menos de 500.000 barris por dia.

• C. Certo
• E. Errado

Observe uma possível seqüência de gráficos de y = ax² + bx + c.

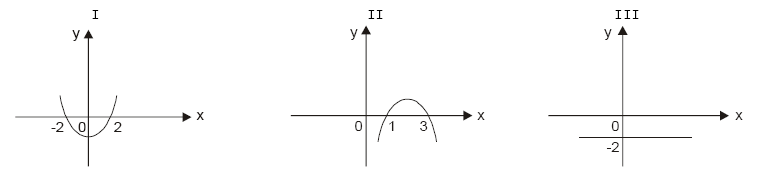
A seguir, observe três caracterizações para as constantes reais a, b e c:

i. a ≠ 0, b ≠ 0 e c ≠ 0
ii. a ≠ 0, b = 0 e c ≠ 0
iii. a = 0, b = 0 e c ≠ 0

A correta correspondência entre gráficos e valores das constantes reais a, b e c é

• A.

  I-i − II-iii − III-ii

• B.

  I-i − II-ii − III-iii

• C.

  I-ii − II-i − III-iii

• D.

  I-ii − II-iii − III-i

• E.

  I-iii − II-i − III-ii

Uma possibilidade para a introdução das idéias da álgebra é a identificação de padrões associada à representação com letras da regularidade observada. Nesse sentido, um professor propôs que seus alunos observassem o seguinte padrão:

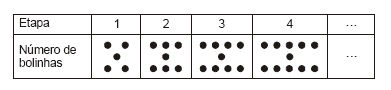
Chamando de E o número da etapa, e de B o número de bolinhas dessa etapa, partindo de caminhos diferentes, quatro alunos apresentaram as seguintes fórmulas para expressar a regularidade observada:

I. B = 2E + 3
II. B = 2 (E + 1) + 1
III. B = 3 (E + 1) − E
IV. B = 3 (E − 1) + 5

Das respostas apresentadas, estão corretas APENAS

• A.

  I e II.

• B.

  I e III.

• C.

  II e III.

• D.

  I, II e III.

• E.

  II, III e IV.

Um importante aspecto que deve ser trabalhado pelo professor no estudo de equações na última série do ensino fundamental refere-se ao seu conjunto universo. Admitindo-se a equação quadrática 2x² + x − 1 = 0, ela terá uma, e somente uma solução, se o seu conjunto universo for

• A.

  N.

• B.

  Z.

• C.

  Q.

• D.

  R-Q.

• E.

  R.

Quando chove na cabeceira do rio Nhundiaquara, na cidade de Morretes, numa determinada época do ano, sabe-se que a taxa simples de crescimento da profundidade do rio devido à chuva é de 25 % por hora, ou seja, na primeira hora de chuva sobe 25% da profundidade inicial, na segunda hora sobe mais 25% da profundidade inicial, na terceira hora sobe mais 25% da profundidade inicial do rio, e assim continua a subir nas horas seguintes, conforme o gráfico abaixo. Considere que a área de secção do rio possa sempre ser tratada como um semicírculo cujo raio r representa a profundidade do rio.

Levando em consideração os dados apresentados, assinale a alternativa que apresenta o tempo necessário para que o rio tenha sua área de secção aumentada de nove vezes a área da secção inicial.

• A.

  4 horas e 50 minutos.

• B.

  6 horas e 30 minutos.

• C.

  5 horas.

• D.

  8 horas.

• E.

  10 horas.

Ainda com relação a fatoração, divisibilidade, razões e proporções, julgue os itens que se seguem.

Considere que a prova objetiva de um concurso público constava de 100 itens do tipo CERTO ou ERRADO e a nota do candidato (N), com base na marcação de sua folha de respostas, era calculada pela fórmula: N = C - E/4, em que C = quantidade de itens marcados na folha de respostas coincidentes com o gabarito oficial definitivo, e E = quantidade de itens marcados na folha de respostas discordantes do gabarito oficial definitivo. Itens não marcados, ou com marcação dupla, não eram considerados. Nessa situação, para que a nota do candidato seja maior ou igual a 50, não fazendo nenhuma dupla marcação e deixando 15 itens sem marcar, o candidato deverá acertar no mínimo 65 itens.

• C. Certo
• E. Errado

Duas Lan Houses (lojas que locam computadores para uso na própria loja) localizadas numa mesma avenida, adotam regime de preços diferentes para locação, dependendo do tempo que o usuário usa o computador. A primeira, L, cobra R$ 3,00 só de entrada e R$ 1,50 por hora de acesso, e a segunda, H, cobra R$ 3,50 por hora e não cobra a entrada. Nesse caso, com o valor pago por 5 horas de uso em L, você pode acessar o computador na loja H, durante

• A.

  7 horas.

• B.

  6 horas.

• C.

  5 horas.

• D.

  4 horas.

• E.

  3 horas.