Questões sobre Progressões/Sequências

Um chefe entregou à sua secretária a tarefa de digitar um relatório de 200 páginas no prazo de 8 dias. No primeiro dia, a secretária digitou 10 páginas e, a partir daí, digitou, em cada dia, tantas páginas quantas havia digitado no dia anterior, mais 4.

Nessas condições, pode-se concluir que a secretária cumpriu com a tarefa no prazo estipulado.

• C. Certo
• E. Errado

• A.

  3.034

• B.

  3.255

• C.

  3.325

• D.

  3.470

• E.

  3.570

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos — 1650 a.C —, envolve a noção de progressão aritmética. "Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a  da soma das outras três." Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Desconsiderando as hipóteses do problema egípcio, dividindo os 100 pães entre os 5 homens de forma que as quantidades recebidas por cada um estejam em uma progressão aritmética de razão 3, então o número máximo de pães que um dos homens receberia é igual a 29.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos — 1650 a.C —, envolve a noção de progressão aritmética. "Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a  da soma das outras três." Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Se b₁ = a, b₂ = a + r, b₃ = a + 2r, b₄ = a + 3r e b₅ = a + 4r são os cinco termos da progressão aritmética, então b₃ + b₄ + b₅ = 3 (b₃ + r).

• C. Certo
• E. Errado

A razão da progressão geométrica das idades é superior a 2/3 .

• C. Certo
• E. Errado

Os números a₃, a₅, e a₆ formam, nessa ordem, uma progressão aritmética.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos - 1650 a.C -, envolve a noção de progressão aritmética.

"Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a 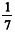da soma das outras três."

 Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Desconsiderando as hipóteses do problema egípcio, dividindo os 100 pães entre os 5 homens de forma que as quantidades recebidas por cada um estejam em uma progressão aritmética de razão 3, então o número máximo de pães que um dos homens receberia é igual a 29.

• C. Certo
• E. Errado

O problema apresentado a seguir, encontrado no Papiro Matemático Rhind ou Ahmos - 1650 a.C -, envolve a noção de progressão aritmética.

"Divida 100 pães por 5 homens, de modo que as quantidades recebidas por cada um estejam em progressão aritmética e que a soma das duas quantidades menores seja igual a 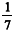da soma das outras três."

 Com base nessas informações e designando por a o termo inicial e por r a razão da progressão aritmética, julgue os itens a seguir.

Se b = a, b = a + r, b = a + 2r, b = a + 3r e b = a + 4r são os cinco termos da progressão aritmética, então b3 + b4 + b5 = 3 (b3 + r).

• C. Certo
• E. Errado

Acerca de contagens, cada um dos próximos itens apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Ao retirar uma senha para ser atendida em uma empresa, uma garota observou que os números eram consecutivos e que seu número era 126. No painel de controle, estava exibido o número 98, cujo portador estava sendo atendido. Nessa situação, no instante descrito faltavam 29 pessoas para serem atendidas, incluindo a garota.

• C. Certo
• E. Errado

Acerca de contagens, cada um dos próximos itens apresenta uma situação hipotética, seguida de uma assertiva a ser julgada.

Um milionário contratou um rapaz para contar as moedas de ouro de sua coleção. Após 5 dias, o rapaz terminou a contagem e declarou que o milionário possuía 66.000 moedas. O rapaz pediu em pagamento 2 das moedas de ouro da coleção do milionário pelo primeiro dia de trabalho, 4 dessas moedas pelo segundo dia de trabalho e assim, sucessivamente, ele deveria receber, nos dias subseqüentes, o valor recebido no dia anterior elevado ao quadrado, até completar os 5 dias trabalhados. Nessa situação, caso aceitasse a proposta e pagasse ao contador, o milionário ficaria com apenas 200 moedas.

• C. Certo
• E. Errado