Questões sobre Progressões/Sequências

Analise a seqüência abaixo.

Nessas condições, quantas vezes o algarismo 1 aparece no resultado de 12 345 678 × 9 + 9?

• A.

  9

• B.

  10

• C.

  11

• D.

  12

• E.

  13

Com relação a progressões e taxas de juros, julgue os seguintes itens.

Considere-se que (a _n ) seja uma seqüência que satisfaz à seguinte relação: a _n + 1- a n = 2 ⁿ e a ₁ = 1. Nesse caso, a ₁ + a ₂ + ... + a ₁₀₀ = 2 ¹⁰¹ - 102.

• C. Certo
• E. Errado

A partir do terceiro termo, cada termo da seqüência a₁, a₂  ,a₃ ,a₄ , ... é a média aritmética dos dois termos imediatamente anteriores. Nesse caso,

se a₅ = 12 e a₆ = 13, então a₁ = 2.

• C. Certo
• E. Errado

A partir do terceiro termo, cada termo da seqüência a₁, a₂  ,a₃ ,a₄ , ... é a média aritmética dos dois termos imediatamente anteriores. Nesse caso,

se a₁ = 1 e a₂ = 17 então a soma dos cinco primeiros termos dessa seqüência é um número racional não-inteiro.

• C. Certo
• E. Errado

Considerando que os números positivos x, y e x + y estão, nessa ordem, em progressão geométrica, julgue os itens a seguir.

A razão dessa progressão é superior a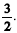

• C. Certo
• E. Errado

Considerando que os números positivos x, y e x + y estão, nessa ordem, em progressão geométrica, julgue os itens a seguir.

Se x for um número racional, então y também será racional.

• C. Certo
• E. Errado

Cinco números estão em progressão aritmética crescente, e o primeiro deles, o segundo e o quinto estão em progressão geométrica. Supondo que todos esses cinco números são maiores que 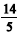 e menores que 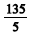e que a razão da progressão aritmética é um número inteiro, julgue os itens seguintes.

O maior desses cinco números é inferior a 25.

• C. Certo
• E. Errado

Cinco números estão em progressão aritmética crescente, e o primeiro deles, o segundo e o quinto estão em progressão geométrica. Supondo que todos esses cinco números são maiores que 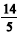 e menores que 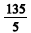e que a razão da progressão aritmética é um número inteiro, julgue os itens seguintes.

A soma desses cinco números é superior a 78.

• C. Certo
• E. Errado

Cinco números estão em progressão aritmética crescente, e o primeiro deles, o segundo e o quinto estão em progressão geométrica. Supondo que todos esses cinco números são maiores que 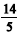 e menores que 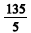e que a razão da progressão aritmética é um número inteiro, julgue os itens seguintes.

A razão da progressão aritmética é o dobro da razão da progressão geométrica.

• C. Certo
• E. Errado

Considere que todos os números inteiros ímpares e positivos podem ser sucessivamente dispostos em linhas e colunas, na forma como é mostrado abaixo.

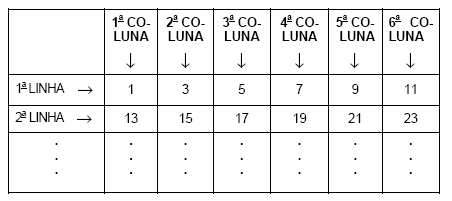
Se fosse possível completar essa tabela, então na quarta coluna e na tricentésima vigésima sétima linha apareceria o número

• A.

  4 021

• B.

  4 015

• C.

  3 937

• D.

  3 919

• E.

  3 847