Questões de Matemática da Fundação CESGRANRIO (CESGRANRIO)

• A.

  30

• B.

  40

• C.

  60

• D.

  120

• E.

  160

• A.

  13%

• B.

  24%

• C.

  30%

• D.

  35%

• E.

  44%

De uma árvore de eucalipto é possível extrair, em média, 85,5kg de celulose. O papel do tipo “A4” é o mais utilizado no mundo e, para produzir 1kg desse papel, são necessários 900g de celulose. Quantas árvores de eucalipto são necessárias para produzir 380kg de papel “A4”?

• A.

  4

• B.

  14

• C.

  16

• D.

  20

• E.

  40

Em 2007, certa empresa de calçados exportou 5/8 de sua produção, vendendo o restante no mercado interno. Assim, as exportações superaram em 3.200 pares as vendas no mercado interno. Quantos pares de calçados essa empresa produziu em 2007?

• A.

  4.800

• B.

  6.400

• C.

  7.200

• D.

  10.400

• E.

  12.800

Em 2007, o nadador brasileiro Thiago Pereira completou a prova "200 medley" em 1min 57s 79 centésimos. Para alcançar o recorde mundial, Thiago precisaria reduzir seu tempo em 2s e 81 centésimos. Qual era, nessa data, o recorde mundial da prova "200 medley"?

• A.

  1min 54s 98 centésimos

• B.

  1min 55s 12 centésimos

• C.

  1min 55s 18 centésimos

• D.

  1min 55s 61 centésimos

• E.

  1min 55s 98 centésimos

O gerente do restaurante de certa empresa fez uma pesquisa e concluiu que os funcionários homens consumiam, em média, 540g por refeição e as mulheres, 450g. Se 60% dos funcionários dessa empresa são homens, qual é, em gramas, o consumo médio, por funcionário, em cada refeição?

• A.

  485

• B.

  495

• C.

  504

• D.

  514

• E.

  525

Dona Maria trouxe um saco de balas de morango e de hortelã para seus filhos, com 100 balas no total. As crianças comeram metade das balas de hortelã e um terço das balas de morango, e ainda restaram 60 balas. Quantas das balas que sobraram eram de hortelã?

• A.

  20

• B.

  30

• C.

  40

• D.

  50

• E.

  60

Considere as três matrizes abaixo.

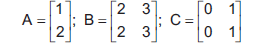
Pode-se afirmar que

• A.

  não é possível somar as matrizes B e C.

• B.

  a matriz B é simétrica.

• C.

  a matriz C é uma matriz identidade.

• D.

  a matriz C é a inversa de B.

• E.

  o produto de matrizes BA é igual a

O gerente de um depósito de bebidas decidiu montar matrizes com dados sobre as vendas de latas de refrigerantes e de cervejas. Em cada elemento m_ij, i indica a semana (1, 2, 3 ou 4) em que foram efetuadas as vendas e j, o tipo de bebida (1 para refrigerante e 2 para cerveja). A matriz abaixo apresenta dados sobre as vendas do mês de março.

Em abril, foram vendidas 350 latas de cerveja a mais e 220 latas de refrigerante a menos que em março. Sabe-se, também, que as vendas de refrigerantes foram menores nas três primeiras semanas do mês, quando comparadas ao mês anterior e que, na 3a semana, foram vendidas mais de 800 latas de cerveja. Dentre as opções abaixo, a única que pode representar a matriz referente às vendas do mês de abril é

• A.
• B.
• C.
• D.
• E.

Em 2006, a diretoria de uma fábrica de autopeças estabeleceu como meta aumentar em 5%, a cada ano, os lucros obtidos com as vendas de seus produtos. Considere que, em 2006, o lucro tenha sido de x reais. Se a meta for cumprida, o lucro dessa empresa, em 2010, será de

• A.

  (0,05)⁴. x

• B.

  (1,05)⁴. x

• C.

  (1,50)⁴ . x

• D.

  (1,20) . x

• E.

  (4,20) . x