Questões de Matemática da Fundação CESGRANRIO (CESGRANRIO)

Observando o calendário de um certo ano, Gabriel percebeu que havia dois meses consecutivos que totalizavam 60 dias. Se esse ano começa em uma segunda-feira, então termina em uma

• A.

  segunda-feira.

• B.

  terça-feira.

• C.

  quarta-feira

• D.

  quinta-feira

• E.

  sexta-feira.

A FAFEN, Fábrica de Fertilizantes Nitrogenados, tem capacidade para produzir, por ano, 2 milhões de toneladas de amônia e de uréia. Se a produção anual de uréia supera em 200 mil toneladas a produção anual de amônia, qual é, em milhões de toneladas, a produção anual de uréia da FAFEN?

• A.

  0,8

• B.

  0,9

• C.

  1,1

• D.

  1,3

• E.

  1,4

No Brasil, é cada vez maior o número de pessoas que pesquisam preços na Internet. O responsável por um site de pesquisa de preços afirmou que, em 2002, o site recebia 2.000 acessos por dia enquanto que, em 2007, esse número subiu para 75.000. Se o aumento anual no número de acessos tivesse ocorrido de forma linear, formando uma progressão aritmética, qual teria sido, em 2006, o número de acessos diários a esse site?

• A.

  34.600

• B.

  45.700

• C.

  56.700

• D.

  60.400

• E.

  61.600

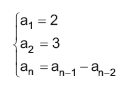
Qual é o 70^o termo da seqüência de números (a_n) definida acima?

• A.

  2

• B.

  1

• C.

  - 1

• D.

  - 2

• E.

  - 3

Nos últimos seis anos, o brasileiro vem trocando o cheque pelo "dinheiro de plástico" e, cada vez mais, efetua pagamentos utilizando cartões de crédito e de débito. O gráfico abaixo apresenta o número de transações efetuadas com cartões no Brasil, de 2000 a 2006.

Os dados acima mostram um aumento linear no número de transações, de 2000 a 2003. Se esse ritmo tivesse sido mantido nos anos seguintes, o número de transações com cartões teria sido, em 2006, x bilhões menor do que realmente foi. Pode-se concluir que x é igual a:

• A.

  1,2

• B.

  1,6

• C.

  2,2

• D.

  2,7

• E.

  3,1

Fichas idênticas são empilhadas de tal forma que, assim que a pilha inicial recebe a sexta ficha, ela é dividida em duas novas pilhas: uma com 4 fichas e outra com 2. A partir daí, as fichas continuam a ser empilhadas, sendo colocadas alternadamente em cada pilha, na ordem decrescente das suas alturas. Assim que alguma das pilhas formadas recebe a sexta ficha, es-sa pilha é dividida em duas novas pilhas, uma com 4, outra com 2 fichas e as fichas continuam a ser empilhadas seguindo o mesmo procedimento.

No momento em que a 19a ficha vai ser colocada, há:

• A. 2 pilhas de 5 fichas e 2 pilhas de 4 fichas.
• B. 2 pilhas de 4 fichas, 2 pilhas de 3 fichas e 2 pilhas de 2 fichas
• C. 1 pilha de 5 fichas, 3 pilhas de 4 fichas, 1 pilha de 3 fichas e 1 pilha de 2 fichas.
• D. 1 pilha de 5 fichas, 2 pilhas de 4 fichas, 2 pilhas de 3 fichas e 1 pilha de 2 fichas
• E. 1 pilha de 5 fichas, 2 pilhas de 4 fichas, 1 pilha de 3 fichas e 1 pilha de 2 fichas.

O mostrador de um relógio digital apresenta quatro dígitos. Cada dígito é formado por sete lâmpadas retangulares. Esse relógio não atrasa e nem adianta. No entanto, o 3º dígito (da esquerda para a direita) do mostrador está com um certo defeito: algumas das lâmpadas que o formam não estão acendendo. Em um certo momento, o tempo que faltava para dar 16h era menor do que o tempo transcorrido desde as 15h. A figura ilustra a aparência do mostrador do relógio nesse momento

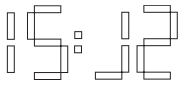
No momento citado,se não houvesse defeito,o3ºdigito mostraria o algarismo:

• A. 0
• B. 2
• C. 3
• D. 4
• E. 5

Um terreno tem a forma de um trapézio isósceles cujas bases medem 40m e 10m e a altura mede 18m. Deseja-se construir um edifício de base retangular com frente sobre a maior base. As dimensões, em metros, que tornam a área construída máxima são:

• A.

  6 e 10

• B.

  6 e 20

• C.

  12 e 20

• D.

  15 e 10

• E.

  18 e 40

Nesse torneio, cada vitória valia 3 pontos, empate valia 1, e derrota não dava ponto algum. É correto afirmar que, ao final do torneio:

• A. o primeiro colocado tinha 8 pontos.
• B. o número de pontos marcados pelo 2o colocado era igual ao número de gols marcados por essa mesma equipe.
• C. a diferença de pontos entre o 1o colocado e o último foi de 7 pontos
• D. uma das equipes teve saldo de gols nulo
• E. todas as equipes marcaram mais de 2 pontos

Chama-se saldo de gols à diferença entre o número de gols marcados e o de gols sofridos. Ao fim do torneio, a soma dos saldos de gols de todas as equipes era:

• A. - 2
• B. - 1
• C. 0
• D. 1
• E. 2