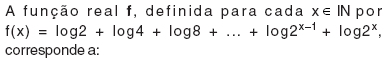Questões de Matemática da Fundação CESGRANRIO (CESGRANRIO)

Se o recruta iniciou seu descanso assim que foi autorizado e a fala do sargento, apresentada no primeiro quadrinho, ocorreu às 15h 45min, a que horas o descanso do recruta deveria ter-se encerrado?

• A.

  13h 35min

• B.

  13h 45min

• C.

  13h 55min

• D.

  14h 05min

• E.

  14h 15min

O ano de 2007 tem 365 dias. O primeiro dia de 2007 caiu em uma segunda-feira. Logo, neste ano, o dia de Natal cairá numa:

• A.

  segunda-feira.

• B.

  terça-feira.

• C.

  quarta-feira.

• D.

  quinta-feira.

• E.

  sexta-feira

Os anos bissextos têm, ao contrário dos outros anos, 366 dias. Esse dia a mais é colocado sempre no final do mês de fevereiro, que, nesses casos, passa a terminar no dia 29. O primeiro dia de 2007 caiu em uma segunda-feira. Sabendo que 2007 não é ano bissexto, mas 2008 será, em que dia da semana começará o ano de 2009?

• A.

  Terça-feira.

• B.

  Quarta-feira.

• C.

  Quinta-feira.

• D.

  Sexta-feira.

• E.

  Sábado.

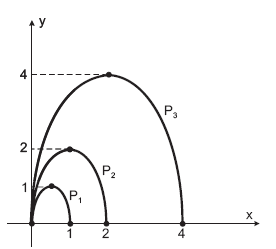
A figura acima ilustra uma seqüência de arcos de parábolas cujas equações são as seguintes:

P₁: y₁ = A₁.x² + B₁.x

P₂: y₂ = A₂.x² + B₂.x

P₃: y₃ = A₃.x² + B₃.x

P₄: y4 = A₄.x²+ B₄.x

......

com y 0 para todas elas. É correto afirmar que A₁₀₁ e B₁₀₁, respectivamente, valem:

• A.
• B.
• C.
• D.
• E.

• A.
• B.
• C.
• D.
• E.

Um tanque de armazenamento de óleo tem a forma de um paralelepípedo retângulo de 5m de comprimento, 2m de largura e 1,5m de profundidade. Este tanque será substituído por um novo tanque de mesmo formato, com a mesma largura e o mesmo comprimento, mas 0,6m mais profundo. O volume, em litros, desse novo tanque será:

• A.

  2.100

• B.

  6.000

• C.

  16.800

• D.

  21.000

• E.

  60.000

Uma circunferência sobre um plano determina duas regiões nesse mesmo plano. Duas circunferências distintas sobre um mesmo plano determinam, no máximo, 4 regiões. Quantas regiões, no máximo, 3 circunferências distintas sobre um mesmo plano podem determinar nesse plano?

• A.

  4

• B.

  5

• C.

  6

• D.

  7

• E.

  8

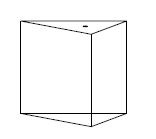
Um tanque de combustível tem a forma de um prisma triangular regular reto, como ilustra a figura acima. Há um pequeno orifício na tampa superior do tanque, exatamente no ponto correspondente ao baricentro. Esse tanque está completamente cheio e será deitado sobre uma superfície horizontal, apoiado em uma das suas faces laterais, de modo que o orifício permitirá o escoamento de parte do combustível. Ao fim do escoamento, a que fração do volume total corresponderá o volume do combustível remanescente no tanque?

• A. 8/27
• B. 4/9
• C. 5/9
• D. 2/3
• E. 19/27

A integral de  é:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

  

A circunferência de equação x² + y² - 2x - 4y = 0 intersecta

 o eixo vertical na origem e no ponto A. A equação da reta que passa por A e pelo centro da circunferência dada é:

• A. 2x - y + 4 = 0
• B. x – y + 4 = 0
• C. x + y – 4 = 0
• D. 2x + y + 4 = 0
• E. 2x + y – 4 = 0