Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Texto para as questões 79 e 80

         A plataforma P-43 da PETROBRAS é uma das maiores plataformas marítimas do mundo. Ela mede 337 m de comprimento e 65 m de altura e a sua produção é de 150 mil barris de óleo por dia.

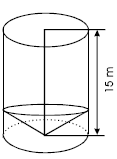
Considere que foram construídos tanques no formato de um cilindro circular reto e a parte inferior é um cone circular reto. A altura total do tanque é de 15 m, sendo de 1,2 m a altura da parte cônica. O raio da parte cilíndrica e da base do cone é igual a 20 m, como ilustrado na figura ao lado. Se um barril de óleo equivale a 158 L, e considerando 3,14 como valor aproximado para é correto afirmar que a quantidade mínima desses tanques necessária para armazenar a produção de um dia da P– 43 é igual a

• A. 2
• B. 3
• C. 4
• D. 5
• E. 6

Portinari utilizou a razão áurea para compor harmoniosamente alguns de seus quadros. Para isto, ele se utilizou de um instrumento análogo ao representado na figura a seguir.

Considerando que os triângulos AFC, AEB e CDB sejam isósceles, de bases AC, AB e CB, respectivamente, e que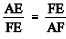 , assinale a opção incorreta.

• A.

  Os triângulos AFC, AEB e CDB são semelhantes.

• B.

  FEDC é um paralelogramo.

• C.

  A razão entre as medidas dos segmentos AC e CB é um número racional.

• D.

  , isto é, o ponto C divide o segmento AB em média extrema razão.

A partir do terceiro termo, cada termo da seqüência a₁, a₂  ,a₃ ,a₄ , ... é a média aritmética dos dois termos imediatamente anteriores. Nesse caso,

se a₁ = 1 e a₂ = 17 então a soma dos cinco primeiros termos dessa seqüência é um número racional não-inteiro.

• C. Certo
• E. Errado

Uma professora distribuiu planificações de poliedros regulares para que seus alunos pintassem as faces seguindo as seguintes regras:

A figura abaixo é a planificação de um desses poliedros, com suas faces numeradas.Com base nas regras apresentadas e na figura, julgue os itens a seguir.

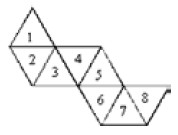
De acordo com as regras, as faces 1 e 6 serão pintadas na mesma cor.

• C. Certo
• E. Errado

Considere a função f definida por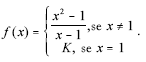

Essa função será continua em todos os reais se K for igual a

• A.

  -1

• B.

  0

• C.

  1

• D.

  2

• E.

  3

Utilizando um programa computacional gráfico, um aluno do ensino médio desenhou, para alguns valores constantes k > 0, o gráfico da função exponencial y = k ax, em que a é uma constante. Esses gráficos estão ilustrados na figura abaixo.

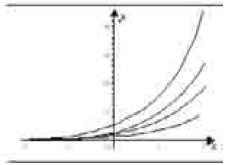
Com base nessas informações e na figura acima, julgue os itens a seguir.

Considere que o aluno tenha desenhado também o gráfico da função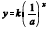   no mesmo sistema de coordenadas. Nesse caso, esse gráfico seria simétrico ao gráfico de y = k ax em relação à reta y = x.

• C. Certo
• E. Errado

Seja S o sistema de duas equações lineares a duas incógnitas, x e y, indicado abaixo, em que a, b, c e d são constantes reais nãonulas e u e v são números reais.

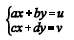
Acerca de S, assinale a opção correta.

• A.

  A inclinação da reta ax +by = u é igual a a/b

• B. No plano cartesiano xOy, a reta cx + dy = v intercepta o eixo das ordenadas no ponto de coordenadas (0,d/v).
• C.

  As retas ax +by = u e cx + dy = v serão paralelas se ab = dc.

• D.

  A condição para que S tenha soluçãoúnica é que as retas ax + by = u e cx + dy = v se interceptem em um único ponto.

• E.

  Se ac = bd, então as retas ax +by = u e cx + dy = v serão perpendiculares.

Considerando que os números positivos x, y e x + y estão, nessa ordem, em progressão geométrica, julgue os itens a seguir.

A razão dessa progressão é superior a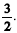

• C. Certo
• E. Errado

Uma professora distribuiu planificações de poliedros regulares para que seus alunos pintassem as faces seguindo as seguintes regras:

A figura abaixo é a planificação de um desses poliedros, com suas faces numeradas.Com base nas regras apresentadas e na figura, julgue os itens a seguir.

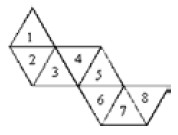
O poliedro cuja planificação corresponde à apresentada na figura acima tem 17 arestas e 11 vértices.

• C. Certo
• E. Errado

Considere uma função f :R→R, satisfazendo às seguintes condições:

Nessa situação, é correto afirmar que a função f

• A.

  possui um mínimo local em x = -1.

• B.

  possui um máximo local em x = 1.

• C.

  é injetiva.

• D.

  possui um máximo local em x = 3.

• E.

  é necessariamente sobrejetiva.