Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)
Lista completa de Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE) para resolução totalmente grátis. Selecione os assuntos no filtro de questões e comece a resolver exercícios.
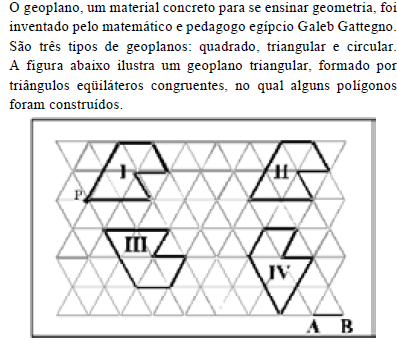
Com base nas informações acima e considerando como unidade de comprimento o comprimento u dos lados dos triângulos que formam a malha do geoplano, julgue os itens a seguir.
O polígono IV é obtido como imagem do polígono I por meio de uma rotação de 60º, no sentido anti-horário em torno do ponto P, seguido de uma translação determinada por um vetor que faz um ângulo de 60º com o segmento AB.
- C. Certo
- E. Errado
Considere o seguinte modelo de programação quadrática.
Considerando as informações fornecidas, julgue os itens que se seguem.
O método do simplex pode ser usado na obtenção da solução do problema dado pelo modelo acima.
- C. Certo
- E. Errado
Considere o seguinte modelo de programação quadrática.
Considerando as informações fornecidas, julgue os itens que se seguem.
A função objetivo pode ser escrita na forma 
, em que H é a matriz hessiana da função q(x).
- C. Certo
- E. Errado
Considere o seguinte modelo de programação quadrática.
Considerando as informações fornecidas, julgue os itens que se seguem.
O valor ótimo da função objetivo é 
.
- C. Certo
- E. Errado
Considere o seguinte modelo de programação quadrática.
Considerando as informações fornecidas, julgue os itens que se seguem.
problema tem infinitas soluções viáveis.
- C. Certo
- E. Errado
Considere o seguinte modelo de programação quadrática.
Considerando as informações fornecidas, julgue os itens que se seguem.
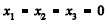é uma solução viável do modelo.
- C. Certo
- E. Errado
Os adeptos da pirataria
As mulheres compram produtos piratas com maior freqüência que os homens. Eles, no entanto, gastam somas mais altas nas bancas de camelôs. É o que mostra uma pesquisa feita em São Paulo pela Fundação Instituto de Administração (FIA), na qual foram entrevistadas 1.260 pessoas, entre homens e mulheres, conforme tabela a seguir.
Com base nessa pesquisa, julgue os itens de 38 a 40.
Suponha que as quantidades de homens e de mulheres entrevistados sejam números diretamente proporcionais a 17 e 13, respectivamente. Nessa situação, entre os entrevistados, mais de 200 mulheres e mais de 220 homens compram produtos piratas.
- C. Certo
- E. Errado
Um vendedor tem nove dias para visitar três cidades —C 1 , C 2 , e C 3 . Os valores obtidos com as vendas feitas em cada cidade dependem do número de dias que ele permanece na cidade e esses valores estão relacionados na seguinte tabela.
De acordo com os dados da tabela, um dia na cidade C 1 gera R$ 40,00, dois dias geram R$ 40,00 mais R$ 30,00 e assim por diante.
Considere que x i , y i e z i sejam variáveis binárias que indicam o número i de dias (i = 1, 2, 3 e 4) que o vendedor deverá passar nas cidades C 1 , C 2 e C 3 , respectivamente. Apenas a título de exemplo, se o vendedor tiver que ficar 2 dias na cidade C 1 , então x 1 = 0, x 2 = 1, x 3 = 0 e x 4 = 0.
Considerando as informações acima, julgue os próximos itens, acerca do modelo de programação linear inteiro associado ao problema descrito.
Como exemplos de métodos para achar a solução ótima de modelos de otimização que pertencem à categoria do modelo considerado, têm-se os métodos dos planos de corte e os métodos branch-and-bound.
- C. Certo
- E. Errado
Um vendedor tem nove dias para visitar três cidades —C 1 , C 2 , e C 3 . Os valores obtidos com as vendas feitas em cada cidade dependem do número de dias que ele permanece na cidade e esses valores estão relacionados na seguinte tabela.
De acordo com os dados da tabela, um dia na cidade C 1 gera R$ 40,00, dois dias geram R$ 40,00 mais R$ 30,00 e assim por diante.
Considere que x i , y i e z i sejam variáveis binárias que indicam o número i de dias (i = 1, 2, 3 e 4) que o vendedor deverá passar nas cidades C 1 , C 2 e C 3 , respectivamente. Apenas a título de exemplo, se o vendedor tiver que ficar 2 dias na cidade C 1 , então x 1 = 0, x 2 = 1, x 3 = 0 e x 4 = 0.
Considerando as informações acima, julgue os próximos itens, acerca do modelo de programação linear inteiro associado ao problema descrito.
O modelo tem 3 variáveis a serem determinadas.
- C. Certo
- E. Errado
Um vendedor tem nove dias para visitar três cidades —C 1 , C 2 , e C 3 . Os valores obtidos com as vendas feitas em cada cidade dependem do número de dias que ele permanece na cidade e esses valores estão relacionados na seguinte tabela.
De acordo com os dados da tabela, um dia na cidade C 1 gera R$ 40,00, dois dias geram R$ 40,00 mais R$ 30,00 e assim por diante.
Considere que x i , y i e z i sejam variáveis binárias que indicam o número i de dias (i = 1, 2, 3 e 4) que o vendedor deverá passar nas cidades C 1 , C 2 e C 3 , respectivamente. Apenas a título de exemplo, se o vendedor tiver que ficar 2 dias na cidade C 1 , então x 1 = 0, x 2 = 1, x 3 = 0 e x 4 = 0.
Considerando as informações acima, julgue os próximos itens, acerca do modelo de programação linear inteiro associado ao problema descrito.
A expressão 
é uma restrição do modelo.
- C. Certo
- E. Errado
O Provas e Concursos é um banco de dados de questões de concursos públicos organizadas por matéria, assunto, ano, banca organizadora, etc
