Questões de Matemática da Centro de Seleção e de Promoção de Eventos UnB (CESPE)

Julgue os itens a seguir.

Considere que, em um frigorífico, 1 kg de frango congelado custe R$ 3,00 e 1 kg de pirarucu, R$ 5,00, e que o proprietário de um restaurante tenha comprado frango e pirarucu em quantidades tais que tenha pago a mesma quantia por cada um desses itens. Então, 65% das quantidades de produtos comprados corresponderam a frango congelado.

• C. Certo
• E. Errado

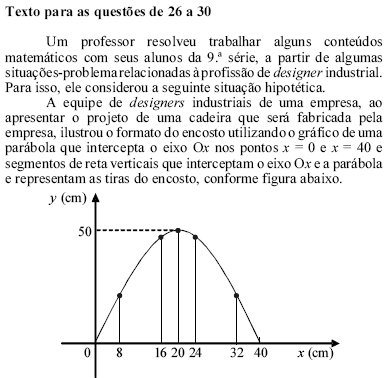
Considere que a equipe de designers referida no texto tenha

• A.

  4

• B.

  8

• C.

  9

• D.

  12

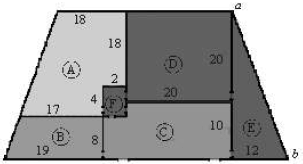
Com base nas informações mostradas na figura acima, que representa esquematicamente a planta baixa de um prédio comercial, em que as dimensões são dadas em metros e a espessura das paredes pode ser considerada desprezível, julgue os itens seguintes

Uma sala circular com a mesma área ocupada pela sala B tem raio inferior a 7 m.

• C. Certo
• E. Errado

Considere que, em uma escola, 5 alunos tenham sido escolhidos para representarem os demais alunos em comissões responsáveis pela organização dos jogos estudantis da região. Se o número de comissões é igual a 5 e um aluno só pode participar de um única comissão, assinale a opção que apresenta o número de maneiras diferentes que os 5 alunos selecionados podem ser distribuídos nas comissões.

• A.

  3.125

• B.

  120

• C.

  25

• D.

  15

No tratamento de modelos que descrevem sistemas complexos ou modelos que não possuem solução analítica, utiliza-se a simulação. Como exemplo, tem-se a manipulação de um modelo matemático de algum sistema real e a observação de seus resultados com o objetivo de dar suporte ao processo de tomada de decisão. Acerca desse tema, julgue os itens subseqüentes.

Por ter alto custo computacional, a aplicação da análise de sensibilidade das variáveis, em geral, deve ser evitada nos modelos de simulação.

• C. Certo
• E. Errado

Para presentear o chefe de departamento de uma empresa por ocasião de seu aniversário, os empregados desse departamento pesquisaram e decidiram comprar um televisor de R$ 480,00, que seriam divididos igualmente entre todos. No momento da cotização, 5 desses empregados argumentaram que se encontravam em dificuldades financeiras e que poderiam pagar apenas a metade da cota inicial de cada um. Dessa forma, coube a cada um dos outros empregados mais R$ 8,00, além da cota inicial.

Com referência à situação hipotética apresentada, e representando por x a quantidade de empregados desse departamento, julgue os próximos itens.

A cota de cada um dos empregados em situação financeira difícil foi superior a R$ 15,00 e a cota de cada um dos demais foi inferior a R$ 45,00.

• C. Certo
• E. Errado

Em cada um dos itens seguintes, é apresentada uma situação hipotética, seguida de uma assertiva a ser julgada.

A quantia de R$ 6.000,00 deve ser repartida entre Paulo e Vanda. Se Paulo receber 2/5 dessa quantia, então Vanda deverá receber R$ 3.600,00.

• C. Certo
• E. Errado

Deseja-se construir um reservatório na forma de um cilindro circular reto, sem tampa superior, com capacidade para 50.000 litros de petróleo. As paredes do reservatório serão feitas de aço com 1 cm de espessura. Esse material será usado tanto na base como nas paredes laterais do reservatório. O objetivo é construir um reservatório que tenha a capacidade exigida e que, na sua construção, necessite da menor quantidade possível de material.

 Julgue os itens que se seguem a respeito desse reservatório, considerando que x e h, em centímetros, sejam, respectivamente, o raio interno da base e a altura interna do cilindro, que correspondem às dimensões do espaço útil do reservatório.

Para ter a capacidade exigida, gastando-se a menor quantidade possível de aço na sua construção, o reservatório deve ser tal que h = 2x.

• C. Certo
• E. Errado

Uma praça, na forma de um triângulo eqüilátero ABC, de lado igual a 5 m, foi dividida em quatro partes, conforme a figura abaixo.

Sabendo que os setores circulares são congruentes e que DE = 1 m, julgue os itens a seguir.

São necessários, no máximo, 18 metros lineares de calçadas para contornar toda a praça e os canteiros.

• C. Certo
• E. Errado

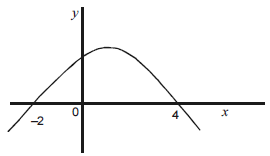
Na figura acima é mostrado, em um sistema de coordenadas cartesianas xOy, o gráfico da função y = f(x) = ax² + bx + c, em que f(-2) = f(4) = 0. Com base nessas informações, no gráfico e na função, é correto afirmar que

• A.

  a > 0.

• B.

  o domínio da função  é o intervalo [-2, 4].

• C.

  c < 0.

• D.

  a figura abaixo representa o gráfico da função y = h(x) =| f(x)| .