Questões de Matemática da Fundação Carlos Chagas (FCC)

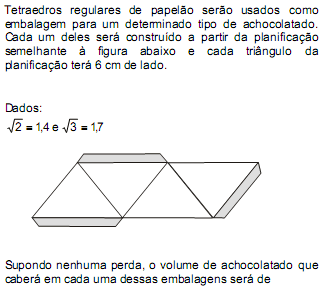
• A. 25,2 mL
• B. 50,4 mL
• C. 75,6 mL
• D. 81,0 mL
• E. 81,6 mL

O gráfico de uma função de 2º grau do tipo f(x) = ax² + bx c está representado na figura abaixo.

Com relação aos coeficientes a, b e c dessa função, pode-se afirmar corretamente que:

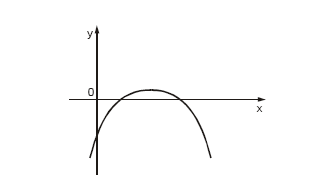
• A. a<0, b>0, c<0
• B. a<0, b=0, c<0
• C. a<0, b<0, c>0
• D. a>0, b>0, c<0
• E. a>0, b<0, c>0

Ao escolher entre uma equação, uma tabela ou um gráfico para representar a dependência entre duas grandezas, como, por exemplo, velocidade e tempo, salário e índice de desconto, ou altura e idade, um aluno está, preferencialmente,

• A.

  analisando e interpretando textos de comunicações de ciência e tecnologia veiculados em diferentes meios.

• B.

  articulando, integrando e sistematizando fenômenos e teorias dentro de uma ciência, entre várias ciências e áreas do conhecimento.

• C.

  analisando, argumentando e posicionando-se criticamente em relação a temas de ciência e tecnologia.

• D.

  lendo, articulando e interpretando símbolos em diferentes linguagens e representações.

• E.

  utilizando adequadamente instrumentos de medidas e de construções geométricas.

Leia atentamente a seguinte situação-problema:

A última pesquisa de intenção de voto, realiza com 2 600 eleitores de todo o país, apontou os seguintes percentuais:

Candidato 1 - 37,5%

Candidato 2 - 28,9%

Candidato 3 - 26,7%

Apesar dos resultados mostrarem a vitória do candidato 1, não há ainda certeza de que isso vá ocorrer, devido a uma série de fatores. Liste e justifique esses fatores que podem influir na alteração dos índices mostrados na pesquisa.

Analise as seguintes competências e habilidades:

I. Representação e comunicação: Interpretar e produzir textos nas diversas linguagens e formas.

II. Investigação e compreensão: Selecionar estratégias de resolução de problemas.

III. Contextualização sócio-cultural: Relacionar etapas da história da Matemática com a evolução da humanidade.

Na resolução eficiente da situação-problema apresentada, um aluno necessariamente mobilizará as competências e habilidades mencionadas em

• A.

  I, II e III.

• B.

  I e II, apenas.

• C.

  I e III, apenas.

• D.

  III, apenas.

• E.

  II, apenas.

A resolução de problemas é peça central para o ensino de Matemática, pois o pensar e o fazer se mobilizam e se desenvolvem quando o indivíduo está engajado ativamente no enfrentamento de desafios. Essa competência não se desenvolve quando propomos apenas exercícios de aplicação dos conceitos e técnicas matemáticas, pois, neste caso, o que está em ação é uma simples transposição analógica: o aluno busca na memória um exercício semelhante e desenvolve passos análogos aos daquela situação, o que não garante que seja capaz de utilizar seus conhecimentos em situações diferentes ou mais complexas.

(MEC, Parâmetros Curriculares Nacionais, Ensino Médio, p.112)

Com base no texto, analise as afirmações abaixo.

I. Na resolução de problemas, o tratamento de situações complexas e diversificadas oferece ao aluno a oportunidade de construir estratégias de resolução e argumentações.

II. O aluno busca na memória passos análogos aos de situações vividas anteriormente, e a aplicação ordenada desses passos garante, com certeza, o sucesso no enfrentamento de situações diferentes ou mais complexas.

III. Resolver um problema exige do aluno, unicamente, leitura cuidadosa e reflexiva.

Dessas afirmações, é correto o que se afirma APENAS em

• A.

  I

• B.

  I e II

• C.

  I e III

• D.

  II e III

• E.

  II

Uma das raízes da equação x4 − 4x3 + 6x2 − 4x = 0 é (1+bi), onde i é a unidade imaginária e b é um número real. As raízes dessa equação são:

• A.

  1 + 2i, 1 − 2i, 1, 0

• B.

  1 + i, 1 − i, −2, 0

• C.

  1 + i, 1 − i, 2, 0

• D.

  1 + 2i, 1 − 2i, 2, 0

• E.

  1 + i, 1 − i, 1, −1

Quando nasceu seu filho, Armando abriu uma poupança e depositou R$ 20,00. Armando fez novos depósitos a cada aniversário do filho, aumentando sempre o valor em R$ 5,00, de um depósito para o outro. Após o depósito referente ao 25o aniversário de seu filho, quanto Armando terá depositado desde o nascimento de seu filho?

• A.

  R$ 2 000,00

• B.

  R$ 2 040,00

• C.

  R$ 2 105,00

• D.

  R$ 2 120,00

• E.

  R$ 2 145,00

Em uma seção há duas funcionárias, uma com 20 anos de idade e a outra com 30. Um total de 150 processos foi dividido entre elas, em quantidades inversamente proporcionais às suas respectivas idades. Qual o número de processos recebido pela mais jovem?

• A.

  90

• B.

  80

• C.

  60

• D.

  50

• E.

  30

Em uma secção, a cada 12 dias, faz-se uma arrumação nos armários e, a cada 15 dias, é feita uma limpeza nos equipamentos, inclusive aos sábados, domingos e feriados. Essas duas tarefas coincidiram no dia 10 de janeiro de 2003. A coincidência seguinte ocorreu no dia

• A.

  15 de fevereiro.

• B.

  20 de fevereiro.

• C.

  01 de março.

• D.

  11 de março.

• E.

  21 de março.

Em certo mês, duas auxiliares entregaram aos analistas um total de 580 correspondências. Se a primeira entregou 68 correspondências a mais do que a segunda, então o número de correspondências entregues pela primeira foi

• A.

  256

• B.

  284

• C.

  296

• D.

  312

• E.

  324