Questões de Matemática da Fundação Carlos Chagas (FCC)

Ao se dividir 95 por x obtém-se o quociente inteiro y e resto da divisão igual a 11. Ao se dividir 210 por x a divisão é exata e o quociente é inteiro e maior do que 10. Sendo assim, pode-se afirmar corretamente que a diferença entre x e y, nessa ordem, é igual a

• A. 14.
• B. 11.
• C. 5.
• D. 21.
• E. 8.

Uma receita para fazer 35 bolachas utiliza 225 gramas de açúcar. Mantendo-se as mesmas proporções da receita, a quantidade de açúcar necessária para fazer 224 bolachas é

• A. 14,4 quilogramas.
• B. 1,8 quilogramas.
• C. 1,44 quilogramas.
• D. 1,88 quilogramas.
• E. 0,9 quilogramas.

Um operador de composições do Metrô faz o trajeto de treinamento em 1 hora, 56 minutos e 40 segundos. Após uma semana de treinamento, esse operador diminuiu o seu tempo em 5%. Sob a orientação de um novo técnico, esse operador diminuiu o seu tempo, aquele já melhorado, em 10%. Desta forma, o tempo inicial para percorrer o trajeto diminuiu, após as duas medições, em

• A. 16 minutos e 55 segundos.
• B. 14 minutos e 21 segundos.
• C. 17 minutos e 30 segundos.
• D. 15 minutos e 35 segundos.
• E. 18 minutos e 48 segundos.

• A. 5/16.
• B. 1/6.
• C. 8/24.
• D. 1/4.
• E. 2/5.

A lei de formação de uma sequência de números é a partir do primeiro termo, um número qualquer diferente de zero, multiplicá-lo por − 4 (quatro negativo) para obter o segundo termo. O terceiro termo é obtido a partir do segundo termo dividindo-o por 2. Alternam-se esses cálculos na obtenção dos termos seguintes, assim o 4o termo é obtido a partir do 3o termo multiplicado por − 4 e segue. A soma dos 13 primeiros termos dessa sequência quando o número inicial for 3 será igual a

• A. 183.
• B. 381.
• C. −192.
• D. 48.
• E. −395.

O diagrama indica a distribuição de atletas da delegação de um país nos jogos universitários por medalha conquistada. Sabe-se que esse país conquistou medalhas apenas em modalidades individuais. Sabe-se ainda que cada atleta da delegação desse país que ganhou uma ou mais medalhas não ganhou mais de uma medalha do mesmo tipo (ouro, prata, bronze). De acordo com o diagrama, por exemplo, 2 atletas da delegação desse país ganharam, cada um, apenas uma medalha de ouro.

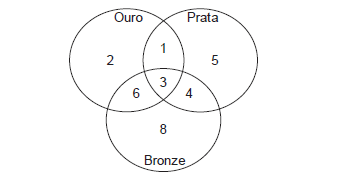
A análise adequada do diagrama permite concluir corretamente que o número de medalhas conquistadas por esse país nessa edição dos jogos universitários foi de

• A. 40.
• B. 15.
• C. 29.
• D. 52.
• E. 46.

O algarismo da milhar do resultado da soma

6+66+666+6666+66666+666666+6666666+66666666+666666666

é igual a

• A. 7.
• B. 0.
• C. 6.
• D. 4.
• E. 8.

Se P e Q são números distintos do conjunto 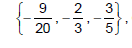então o maior valor possível de P−Qé:

• A. 3/10.
• B. 3/20.
• C. 13/60.
• D. -21/20.
• E. -19/15.

Quatro números inteiros serão sorteados. Se o número sorteado for par, ele deve ser dividido por 2 e ao quociente deve ser acrescido 17. Se o número sorteado for ímpar, ele deve ser dividido por seu maior divisor e do quociente deve ser subtraído 15. Após esse procedimento, os quatro resultados obtidos deverão ser somados. Sabendo que os números sorteados foram 40, 35, 66 e 27, a soma obtida ao final é igual a

• A. 63.
• B. 87.
• C. 59.
• D. 28.
• E. 65.

O resultado da expressão:

(4 − 7)² ⋅ (4 − 6)³ ⋅ (4 − 5)⁴ − (5 − 8)² ⋅ (5 − 7)³ ⋅ (5 − 6)⁵

é igual a

• A. 192.
• B. 144.
• C. − 192.
• D. 0.
• E. − 144.