Questões de Matemática da Fundação Carlos Chagas (FCC)

Um painel de operação do Metrô necessita 24 horas diárias de monitoramento. Um turno de trabalho de Lúcia no monitoramento desse painel é das 22:38 do dia 08/10/2013 até 02:46 do dia 09/10/2013. Durante esse turno de trabalho Lúcia é obrigada a parar para descanso, sendo substituída por Marisa por 10 minutos. Se a parada de descanso de Lúcia divide seu tempo de trabalho no monitoramento em duas metades idênticas, então a parada se inicia no dia 09/10/2013 às

• A. 01:02.
• B. 00:37.
• C. 00:42.
• D. 02:04.
• E. 01:59.

O resultado dessa expressão numérica:

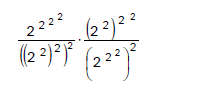
é igual a

• A. 512.
• B. 1.
• C. 256.
• D. 128.
• E. 64.

O resultado da expressão numérica 5³ ÷ 5 . 5⁴ ÷ 5 . 5⁵ ÷ 5 ÷ 5⁶ − 5 é igual a

• A. 120.
• B. 1/5.
• C. 55.
• D. 25.
• E. 620.

Um jogo de vôlei entre duas equipes é ganho por aquela que primeiro vencer três sets, podendo o placar terminar em 3 a 0, 3 a 1 ou 3 a 2. Cada set é ganho pela equipe que atingir 25 pontos, com uma diferença mínima de dois pontos a seu favor. Em caso de igualdade 24 a 24, o jogo continua até haver uma diferença de dois pontos (26 a 24, 27 a 25, e assim por diante). Em caso de igualdade de sets 2 a 2, o quinto e decisivo set é jogado até os 15 pontos, também devendo haver uma diferença mínima de dois pontos. Dessa forma, uma equipe pode perder um jogo de vôlei mesmo fazendo mais pontos do que a equipe adversária, considerando-se a soma dos pontos de todos os sets da partida. O número total de pontos da equipe derrotada pode superar o da equipe vencedora, em até

• A. 44 pontos.
• B. 50 pontos.
• C. 19 pontos.
• D. 25 pontos.
• E. 47 pontos.

Amanda utiliza pequenas caixas retangulares, de dimensões 20 cm por 20 cm por 4 cm, para embalar as trufas de chocolate que fabrica em sua casa. As trufas são redondas, tendo a forma de bolas (esferas) de 4 cm de diâmetro. Considerando que as caixas devem ser tampadas, a máxima quantidade de trufas que pode ser colocada em uma caixa desse tipo é igual a

• A. 32.
• B. 25.
• C. 20.
• D. 16.
• E. 12.

Um laboratório de produtos farmacêuticos possui cinco geradores que mantêm o funcionamento dos equipamentos mesmo quando há falta de energia elétrica. A partir do momento em que o fornecimento de energia é interrompido, esses geradores são ativados, operando em forma de revezamento por períodos de tempo diferentes, conforme sua capacidade. A tabela mostra o sistema de revezamento nas primeiras 24 horas após a queda de energia.

O ciclo de revezamento descrito repete-se a cada 24 horas, até que a energia seja restabelecida. Suponha que o fornecimento de energia elétrica tenha sido interrompido por 15 dias seguidos. O gerador que estava em funcionamento 307 horas após a queda de energia era o gerador

• A. I.
• B. II.
• C. III.
• D. IV.
• E. V.

Em uma escola de 100 alunos, há três recuperações durante o ano, sendo uma em cada trimestre. Em certo ano, 55 alunos ficaram em recuperação no 1o trimestre, 48 no 2o e 40 no 3o. Somente com esses dados, é correto concluir que naquele ano, necessariamente,

• A. todos os alunos da escola ficaram em recuperação em, pelo menos, um trimestre.
• B. 40 alunos ficaram em recuperação em dois trimestres e os demais em um único.
• C. pelo menos um aluno da escola ficou em recuperação em somente dois trimestres.
• D. no mínimo 5 e no máximo 40 alunos ficaram em recuperação nos três trimestres.
• E. pelo menos 3 alunos ficaram em recuperação no 1o e também no 2o trimestre.

Partindo do ponto A, um automóvel percorreu 4,5 km no sentido Leste; percorreu 2,7 km no sentido Sul; percorreu 7,1 km no sentido Leste; percorreu 3,4 km no sentido Norte; percorreu 8,7 km no sentido Oeste; percorreu 4,8 km no sentido Norte; percorreu 5,4 km no sentido Oeste; percorreu 7,2 km no sentido Sul, percorreu 0,7 km no sentido Leste; percorreu 5,9 km no sentido Sul; percorreu 1,8 km no sentido Leste e parou. A distância entre o ponto em que o automóvel parou e o ponto A, inicial, é igual a

• A. 7,6 km.
• B. 14,1 km.
• C. 13,4 km.
• D. 5,4 km.
• E. 0,4 km.

Ao ritmo de consumo médio de água per capita de uma casa com 3 habitantes, um total de 4 m³ de água dura exatos 5 dias. Com 1 habitante a mais na casa, e mantido o mesmo consumo médio de água per capita, os mesmos 4 m³ de água vão durar, no máximo,

• A. 3 dias e 18 horas.
• B. 4 dias e 12 horas.
• C. 4 dias e 16 horas.
• D. 3 dias e 7 horas.
• E. 4 dias e 2 horas.

Partindo de um ponto inicial A, Laura caminhou 4 km para leste, 2 km para sul, 3 km para leste, 6 km para norte, 6 km para oeste e, finalmente, 1 km para sul, chegando no ponto B. Artur partiu do mesmo ponto A de Laura percorrendo X km para norte e 1 km para a direção Y, chegando no mesmo ponto B em que Laura chegou. Sendo Y uma das quatro direções da rosa dos ventos (norte, sul, leste ou oeste), X e Y são, respectivamente,

• A. 6 e sul.
• B. 2 e norte.
• C. 4 e oeste.
• D. 3 e leste.
• E. 4 e leste.