Questões de Matemática da Núcleo de Computação Eletrônica UFRJ (NCE)

Carlos e Luisa receberam no total R$ 1.935,00 por um trabalho que realizaram. Luisa receberá 15% a mais que Carlos, já que trabalhou mais. A quantia que Luisa irá receber a mais do que Carlos é:

• A. R$ 135,00;
• B. R$ 252,00;
• C. R$ 290,25;
• D. R$ 405,00;
• E. R$ 900,00.

Para organizar os processos da firma em que trabalha, Paulo vai comprar alguns arquivos com quatro gavetas cada. Estimando que em cada gaveta caibam 35 processos e que Paulo tenha 1890 processos para guardar, o número mínimo de arquivos que necessita encomendar é:

• A. 12;
• B. 13;
• C. 14;
• D. 54;
• E. 55.

Mariana telefonou para uma loja a fim de encomendar 350 salgadinhos para a sua festa. No ato da encomenda, o atendente trocou o algarismo 5 pelo 7 ao escrever o número. Assim, o número de salgadinhos que Mariana recebeu a mais foi:

• A. 2;
• B. 5;
• C. 7;
• D. 20;
• E. 50.

Um nanômetro é, por definição, um bilionésimo de um metro. Antônio Maria tem 1,64m de altura. A altura de Antônio Maria em nanômetros é igual a:

• A. 0,000000164;
• B. 1,64;
• C. 16.400.000;
• D. 164.000.000;
• E. 1.640.000.000.

Avalie se os quatro números a seguir são divisíveis por

3: 300 ; 333.333.333 ; 3.444.444.444.444.444 ;

11.111.111.111.111.111.111.111.111.111

A quantidade de números divisíveis por 3 é:

• A. 0;
• B. 1;
• C. 2;
• D. 3;
• E. 4;

O resultado d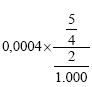e  é:

• A. 0,25;
• B. 1;
• C. 40;
• D. 200;
• E. 5.000.

Uma obra será financiada pelo governo estadual em parceria com uma empresa privada e com um banco. Sabe-se que:

O mínimo que o governo estadual deverá investir nesta obra, em milhões de reais, é:

• A. 3
• B. 4
• C. 5
• D. 6
• E. 7

A tabela abaixo apresenta a produção de gás em função do tempo de um estado.

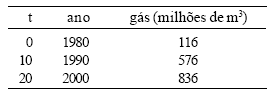
 Supondo-se que o volume de gás V produzido ao longo do tempo seja modelado pela equação V( t ) = at² + bt + c, o volume máximo de produção de gás será atingido no ano de:

• A. 2008
• B. 2009
• C. 2010
• D. 2011
• E. 2012

A altura de Maria é medida no primeiro dia de janeiro de cada ano e registrada para acompanhar o seu crescimento. No dia 1º de janeiro de 2005, quando tinha 10 anos, ela media 1,38 m e no dia 1º de janeiro de 2007 ela media 1,50m. Supondo-se, para fins de estimativa, que o seu crescimento seja linear no período de 10 até 14 anos, em 1° de janeiro de 2008 Maria vai medir:

• A. 1,54m;
• B. 1,56m;
• C. 1,62m;
• D. 1,68m;
• E. 1,74m.

Em relação aos extremos relativos de f ( x ) = x³ – 3x² + 3 é correto afirmar que:

• A.

  em x = 0 ocorre um máximo relativo e em x = 2 ocorre um mínimo relativo;

• B.

  em x= 0 ocorre um mínimo relativo e em x = 3 ocorre um máximo relativo;

• C.

  em x = 2 ocorre um mínimo relativo e em x = 12 ocorre um máximo relativo;

• D.

  em x = - 1 ocorre um máximo relativo e em x = 5 ocorre um mínimo relativo;

• E.

  em x = 4 ocorre um máximo relativo e em x = 12 ocorre um mínimo relativo.