Questões de Matemática da Núcleo de Computação Eletrônica UFRJ (NCE)

Carlos tinha um conjunto de canetas que comprou a R$ 0,65 cada. Perdeu três e vendeu o restante ao seu primo por R$ 1,10 cada, obtendo R$ 2,10 de lucro. O número de canetas que Carlos vendeu ao seu primo foi:

• A.

  8

• B.

  9

• C.

  10

• D.

  11

• E.

  12

A soma de todos os números da forma 3ⁿ,

• A.

  (1 + 3¹⁰) . 5;

• B.

  (3 + 3¹⁰) . 5;

• C.
• D.
• E.

Uma prova de 50 questões objetivas foi elaborada de tal modo que o nível de dificuldade é crescente; assim, cada questão vale 2 pontos a mais que a questão anterior. Se o valor da primeira questão é 1, o número máximo de pontos que se pode obter nessa prova é:

• A.

  1 300;

• B.

  1 325;

• C.

  2 475;

• D.

  2 500;

• E.

  2 525.

A quantidade de números ímpares entre 100 e 999 com todos os algarismos distintos é:

• A.

  320

• B.

  360

• C.

  405

• D.

  450

• E.

  500

Três números inteiros, M, N e O, quando decompostos em fatores primos, podem ser escritos como

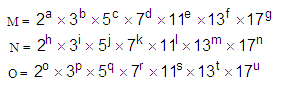
onde os expoentes a, b, ..., h, i, ..., o, p, ..., u são todos números inteiros positivos.

Nesse caso, NÃO é correto afirmar que:

• A.

  M, N e O são divisíveis por 210;

• B.
• C.

  M pode ser múltiplo de N e de O;

• D.

  M, N e O não são múltiplos de 31;

• E.

  

Ao fazer uma divisão entre dois números inteiros, numa calculadora, Josimar obteve, no visor, como resultado, 0,1234123412341234. Assinale o item que pode indicar a divisão feita por Josimar:

• A.

  

• B.

  

• C.

  

• D.

  

• E.

Em uma interseção de quatro ramos, sabendo-se que ambas as vias possuem mão dupla de direção e que somente os movimentos de seguir em frente, girar à direita e girar à esquerda são permitidos em cada aproximação, assinale o número total de conflitos de divergência, convergência e cruzamentos, respectivamente:

• A. 16; 16; 8;
• B. 8; 8; 32;
• C. 8; 16; 32;
• D. 16; 8; 8;
• E. 8; 8; 16.

No triângulo ABC , Â = 90o e AD é a altura relativa ao lado BC. Sabendo-se que BD = 2 cm e AD = 4 cm , o valor de CD, em centímetros, é:

• A.

  

• B.

  

• C.
• D.
• E.

Num campeonato de futebol, a vitória numa partida vale três pontos para o vencedor e nenhum ponto para o perdedor; em caso de empate, cada equipe ganha um ponto. Um campeonato foi disputado por oito equipes, em turno e returno, de modo que cada equipe jogou duas vezes com cada uma das demais. Das partidas jogadas, exatamente vinte e duas terminaram empatadas. Nesse caso, se somarmos os totais de pontos obtidos, por cada equipe, obteremos:

• A.

  130;

• B.

  146;

• C.

  168;

• D.

  190;

• E.

  222.

O custo de mão-de-obra de manutenção (CMOM) do parque de material rodante de uma ferrovia, para cada veículo k, em cada atividade de manutenção m, na qual se emprega pessoal capacitado na função h, sendo HA a quantidade de pessoal empregada anualmente e SA o salário anual médio do pessoal, é dado pela expressão:

• A.
• B.
• C.
• D.
• E.