Questões de Matemática da Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP)

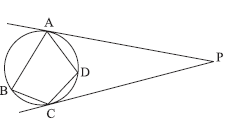
Na figura, as retas PA e PC são tangentes à circunferência, e o ângulo APC mede 50º. As medidas dos ângulos ABC e ADC são, respectivamente,

• A.

  90º e 90º.

• B.

  80º e 100º.

• C.

  75º e 105º.

• D.

  70º e 110º.

• E.

  65º e 115º.

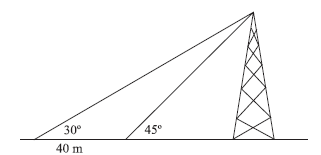
Um observador em uma planície vê ao longe uma torre de transmissão segundo um ângulo de 30º (vide figura).

Após caminhar uma distância de 40 m em direção à torre, ele passa a vê-la segundo um ângulo de 45º. A altura da torre é, aproximadamente, de

• A.

  45 m.

• B.

  55 m.

• C.

  64 m.

• D.

  80 m.

• E.

  94 m.

Uma fábrica de chocolates está fazendo barrinhas na forma de um prisma triangular, cujas dimensões estão indicadas na figura.

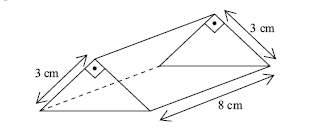
Sabendo que 1 cm³ de chocolate pesa aproximadamente 1,3 gramas, o número máximo de barrinhas desse tipo que é possível fabricar com 1 kg de chocolate é

• A.

  17.

• B.

  19.

• C.

  21.

• D.

  23.

• E.

  25.

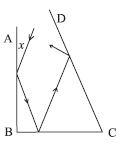
Quando um raio de luz é refletido em uma superfície lisa, o ângulo formado pelo raio incidente com a superfície é congruente ao ângulo formado pelo raio refletido com a superfície. Na figura, os ângulos ABC e BCD medem, respectivamente, 90º e 70º e o raio incidente faz um ângulo de medida x = 30º com a superfície AB. Sob que ângulo o raio incide em AB na segunda vez?

• A.

  40º.

• B.

  50º.

• C.

  60º.

• D.

  70º.

• E.

  80º.

O conjunto dos pontos do plano cartesiano tais que sua distância ao ponto (1, 2) é sempre igual à metade de sua distância à reta de equação x + 2 = 0 é

• A.

  uma reta.

• B.

  duas retas paralelas distintas.

• C.

  uma elipse.

• D.

  uma parábola.

• E.

  uma hipérbole.

Num plano cartesiano, uma circunferência de equação x² + y² + ax + by = 24 passa pelos pontos (2,2) e (4,0). Pode-se afirmar que o centro da circunferência está no

• A.

  primeiro quadrante, e o raio é maior do que 1.

• B.

  primeiro quadrante, e o raio é menor do que 1.

• C.

  terceiro quadrante, e o raio é menor do que 1.

• D.

  terceiro quadrante, e o raio é maior do que 1.

• E.

  quarto quadrante, e o raio é maior do que 1.

A figura mostra uma caixa de madeira, sem tampa, com a forma de um bloco reto-retângulo. Para que o volume dessa caixa seja 1 m³, a medida x deverá ser igual a

• A. 50 cm.
• B. 80 cm.
• C. 100 cm.
• D. 110 cm.
• E. 120 cm.

Assinale a alternativa que apresenta, corretamente, os números que completam a seqüência dada.

• A.

  6088 – 6092 – 6094 – 6100.

• B.

  6087 – 6093 – 6095 – 6101.

• C.

  6087 – 6092 – 6095 – 6101.

• D.

  6080 – 6093 – 6094 – 6000.

Uma criança dispõe de 10 lápis de cores diferentes e, para pintar um desenho, precisa utilizar pelo menos 4 cores diferentes. No entanto, a professora lançou um desafio para ver quem consegue pintar, da melhor maneira possível esse desenho, usando no máximo 7 cores diferentes. Nessas condições, o número de maneiras distintas de pintar esse desenho é

• A.

  210.

• B.

  420.

• C.

  548.

• D.

  664.

• E.

  792.

Assinale a afirmação verdadeira.

• A.

• B.

• C.

• D.

• E.