Questões de Matemática da Fundação para o Vestibular da Universidade Estadual Paulista (VUNESP)

O valor de um prêmio de loteria foi totalmente dividido entre Camilo e Sávio na razão de 9 para 8, nessa ordem. Sabendo-se que Camilo recebeu R$ 20.000,00 a mais que Sávio, é correto afirmar que o valor total desse prêmio foi igual a

• A. R$ 180.000,00.
• B. R$ 220.000,00.
• C. R$ 260.000,00.
• D. R$ 320.000,00.
• E. R$ 340.000,00.

O número de funcionários que deveriam assistir à projeção de um audiovisual corporativo era 80% maior que o número de assentos disponíveis no auditório da empresa. Decidiu-se, então, dividir esses funcionários em dois grupos de igual número e fazer duas sessões. Sabendo- -se que todos os funcionários assistiram à apresentação e que, em cada sessão, restaram 5 assentos vazios, é correto afirmar que o número de assentos disponíveis nesse auditório era igual a

• A. 50.
• B. 55.
• C. 60.
• D. 75.
• E. 80.

Em uma indústria, 5 máquinas iguais, de mesmo rendimento, produzem n unidades de certo produto em 9 horas de funcionamento ininterrupto. Se a empresa passar a operar com somente 4 dessas máquinas, o tempo de funcionamento necessário para produzir n unidades desse mesmo produto será de

• A. 12h e 10min.
• B. 11h e 25min.
• C. 11h e 15min.
• D. 10h e 50min.
• E. 10h e 25min.

Walter e Xavier emprestaram, juntos, um total de R$ 8.000,00 para seu amigo Tadeu, sem cobrança de juros, sendo que a quantia emprestada por Xavier foi R$ 1.600,00 maior que a de Walter. Valendo-se de seu 13o salário, Tadeu fez um pagamento de valor igual a R$ 6.500,00, sendo essa quantia dividida entre Walter e Xavier de forma diretamente proporcional aos respectivos valores emprestados. Para que o valor emprestado por Xavier seja totalmente quitado, ainda faltam

• A. R$ 600,00.
• B. R$ 700,00.
• C. R$ 800,00.
• D. R$ 900,00.
• E. R$ 1.000,00.

Para se classificar para a segunda fase de certo concurso, um candidato deveria acertar, no mínimo, 3/4 das questões da prova objetiva da primeira fase. Arnaldo, que fez a prova, deu respostas erradas para 3/8 das questões. Constatou, então, que, se tivesse acertado 5 questões a mais do que efetivamente acertou, teria obtido o número de acertos mínimo para se classificar para a fase seguinte. O número de questões que Arnaldo acertou, nessa prova, foi igual a

• A. 12.
• B. 15.
• C. 18.
• D. 20.
• E. 25.

Na sequência numérica –2, 0, –3, 1, – 4, 2, –5, 3, –6, ..., o primeiro elemento é –2. Mantendo-se a regularidade, o trigésimo segundo elemento dessa sequência será

• A. 13.
• B. 14.
• C. 15.
• D. 16.
• E. 17.

Uma pesquisa foi feita em um grupo de profissionais formados em Matemática ou Física ou Química, e somente nessas áreas. O resultado da pesquisa mostrou que apenas 3 desses profissionais têm as três formações, que exatamente 5 têm formações apenas em Matemática e em Física, exatamente 7 têm formações apenas em Matemática e em Química, e exatamente 12 têm formações apenas em Química e em Física. Mostrou, também, que somente 25 desses profissionais têm formação em Matemática, somente 25 têm formação em Física e somente 24 têm formação em Química. Sendo assim, o número total de pessoas que compõem esse grupo é

• A. 43.
• B. 44.
• C. 45.
• D. 46.
• E. 47.

Para a festa de confraternização de fim de ano uma empresa separou uma certa quantia para ser distribuída igualmente entre todos os colaboradores presentes à festa. Se os 4 colaboradores que não participaram tivessem ido à festa, cada colaborador teria recebido R$ 20,00 a menos; por outro lado, se, do total de colaboradores, 13 deixassem de participar, cada colaborador presente à festa teria recebido R$ 60,00 a mais. O valor destinado pela empresa para essa festa foi de

• A. R$ 10.560,00.
• B. R$ 11.040,00.
• C. R$ 11.520,00.
• D. R$ 12.000,00.
• E. R$ 12.480,00.

Dois reservatórios de água têm formato de paralelepípedo. Um tem por base interna um quadrado de 2 m de lado, e o outro tem por base interna a forma de um retângulo de medidas 1,5 m por 2 m. No domingo passado, ambos armazenavam 12 000 L de água e, no dia seguinte, foram retirados de cada um deles 3 000 L de água, fazendo com que a diferença de altura da coluna de água entre esses reservatórios, em cm, ficasse igual a

• A. 75.
• B. 90.
• C. 105.
• D. 120.
• E. 135.

Um quadrado tem um vértice em comum com um retângulo e outro vértice pertencendo a um dos lados desse retângulo, conforme mostra a figura, que não está em escala.

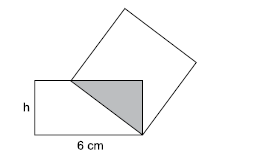
Esses dois polígonos determinam um triângulo cuja área é igual a 24% da área do quadrado. Esse retângulo tem lados de medida h e 6 cm, e sua área mede 3 vezes a área do triângulo determinado. De acordo com essas condições, o maior valor possível que pode assumir h, em cm, é igual a

• A. 2
• B. 3
• C. 7/2
• D. 4
• E. 16/3