Questões sobre Planejamento de Ensino

A professora trouxe um mapa dos arredores da escola. Após o estudo detalhado do mapa e de todas as possibilidades, pediu que os alunos indicassem o melhor caminho para irem da escola ao museu de ciências.

A indicação foi feita da melhor maneira possível. A expectativa de aprendizagem é:

• A.

  utilizar unidades usuais de comprimento, massa e capacidade.

• B.

  descrever, interpretar e representar por meio de desenhos a localização ou movimentação de uma pessoa ou um objeto.

• C.

  utilizar dados apresentados de maneira organizada, por meio de tabelas simples ou tabelas de dupla entrada.

• D.

  resolver situações-problema que envolvam o significado de unidades de medidas de superfície.

• E.

  compor e decompor figuras planas e identificar que qualquer polígono pode ser composto a partir de figuras triangulares.

O professor de Educação Física mede a altura (em metros) e verifica o peso (em quilogramas) de todos os alunos no início do ano. Os dados de todos os alunos são anotados numa tabela e projetados na sala de aula. Pergunta-se:

− Quem é o aluno mais alto da turma? E o mais baixo?

− Quem possui o maior peso? E o menor?

Ao responder a essas questões, os alunos cumpriram o objetivo de

• A.

  interpretar e operar com números racionais.

• B.

  formular e resolver situações-problemas, compreendendo diferentes significados da multiplicação e divisão envolvendo números racionais na forma decimal.

• C.

  comparar e ordenar números racionais de uso frequente, nas representações decimais.

• D.

  resolver operações com números racionais utilizando-se da decomposição dos mesmos.

• E.

  resolver operações por meio de cálculo mental ou por técnica operatória convencional, buscando estratégias de verificação e controle de resultados pelo uso de estimativa e/ou da calculadora.

Essa atividade visa verificar

• A.

  a compreensão e resolução dos problemas no campo aditivo ou no multiplicativo

• B.

  a compreensão da sucessão de números naturais.

• C.

  o estabelecimento da relação parte do todo e razão.

• D.

  a leitura e a interpretação de números arredondados, da forma como aparecem nos diferentes portadores.

• E.

  a compreensão e utilização das regras do sistema de numeração decimal para interpretar e produzir números de qualquer ordem de grandeza.

A professora entregou a todos os alunos quatro folhas de papel sulfite com 10 × 10 quadradinhos. Pediu que pintassem na

− 1ª folha, 10 quadradinhos de amarelo;

− 2ª folha, 20 quadradinhos de vermelho;

− 3ª folha, 25 quadradinhos de azul;

− 4ª folha, 50 quadradinhos de verde.

Após a representação fracionária e associação dos quadradinhos a uma amostra, espera-se que os alunos sejam capazes de

• A.

  identificar as possíveis maneiras de combinar elementos de uma coleção de objetos e contabilizá-las usando estratégias pessoais.

• B.

  explorar a ideia de probabilidade em situações-problema simples.

• C.

  calcular o resultado da adição de números racionais na forma fracionária, por meio de estratégias pessoais e pelo uso de técnicas operatórias convencionais.

• D.

  calcular perímetro de figuras desenhadas em malhas quadriculadas ou não.

• E.

  entender que porcentagem indica uma parte em relação a 100 e iniciem a representação por meio do uso correto de %.

Num dia de pesquisa no laboratório de informática uma dupla de alunos copiou em seus cadernos:

A leitura desse texto favorece a

• A.

  reflexão sobre as regularidades dos números racionais, verificando que as regras de organização dos números naturais não valem para os decimais, seja na sua forma de representação decimal ou fracionária.

• B.

  análise de situações-problema que envolvem operações comerciais e a partir delas tomar decisões considerando as vantagens que se teria em cada situação.

• C.

  colocação em jogo dos conhecimentos construídos sobre os números racionais, para poder compará-los.

• D.

  compreensão e uso das regras do sistema de numeração decimal, para leitura e escrita, comparação, ordenação e arredondamento de números naturais de qualquer ordem de grandeza.

• E.

  escrita de números racionais de uso frequente nas representações fracionária e decimal e localização deles na reta numérica.

Durante a aula foi apresentada a receita de um bolo:

BOLO DE CENOURA

1 xícara de óleo

2 colheres de sopa de fermento em pó

2 xícaras de açúcar

3 ovos

3 xícaras de farinha de trigo

4 cenouras médias descascadas e fatiadas

Modo de fazer:

Bata o açúcar, os ovos e o óleo no liquidificador. Numa vasilha, despeje a mistura e acrescente a farinha de trigo e o fermento em pó. Coloque a massa numa assadeira untada e enfarinhada e asse em forno pré-aquecido por 45 minutos. A receita rende 20 porções.

Para uma sala de 30 alunos, a professora propôs as seguintes questões:

− Uma receita será suficiente para todos?

− Levando-se em conta que a receita não aceita redução (não há como dividir ovos ao meio) e que todos os alunos consumam uma porção, quantas receitas deverão ser feitas, no mínimo?

− Considerando-se a quantidade mínima de receitas, quantos pedaços de bolo sobrarão?

Espera-se que, com a realização dessa atividade, a professora verifique se os alunos são capazes de

• A.

  analisar, interpretar, e formular situações-problema, compreendendo diferentes significados das operações com números naturais.

• B.

  resolver diferentes operações com números naturais, por meio de estratégias pessoais e do uso de técnicas operatórias convencionais, do cálculo mental, e usar estratégias de verificação e controle de resultados pelo uso do cálculo mental ou da calculadora.

• C.

  comparar e ordenar números racionais de uso frequente nas representações fracionária e decimal.

• D.

  identificar e produzir frações equivalentes, pela observação de representações gráficas e de regularidades nas escritas numéricas.

• E.

  reconhecer e fazer leitura de números racionais no contexto diário nas representações fracionária e decimal.

A professora de 3º ano apresentou a seguinte situação-problema:

Leonardo é 6 anos mais velho que João, que tem 5 anos.

Quantos anos Leonardo tem? Em relação ao campo aditivo, o problema citado relaciona-se essencialmente com o significado de:

• A.

  composição.

• B.

  transformação.

• C.

  comparação.

• D.

  representação.

• E.

  estimativas.

Em uma aula do 4º ano, após discutir a importância da reciclagem para o meio ambiente, a professora solicitou que os alunos trouxessem as embalagens utilizadas em casa nos últimos 5 dias (latas de leite e de molhos, caixas de sapatos, de creme dental, entre outras). Com isso, além de explorar os aspectos citados, ela também pode

• A.

  observar as características de cada uma das formas, diferenciando-as em dois grandes grupos: corpos redondos e poliedros.

• B.

  ampliar e reduzir figuras planas pelo uso de malhas quadriculadas.

• C.

  compor e decompor figuras planas e identificar que qualquer polígono pode ser composto a partir de figuras triangulares.

• D.

  identificar semelhanças e diferenças entre polígonos, considerando seu número de lados ou ângulos.

• E.

  descrever, interpretar e representar a localização ou a movimentação de um objeto por meio de desenhos.

Pede-se a todos os alunos de 5º ano que preencham uma ficha com os seguintes dados:

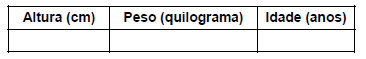
Em sala de aula montam-se três painéis coletivos: de altura, de peso e de idade.

Divide-se a sala em três grupos e cada grupo representa os dados de maneira diferente:

− a altura em gráfico de colunas;

− o peso em gráfico de barras;

− a idade em gráficos de setor.

Nessa atividade, as expectativas de aprendizagem estão agrupadas, principalmente, nos seguintes blocos temáticos:

• A.

  números e operações.

• B.

  operações e grandezas e medidas.

• C.

  espaço e forma e tratamento da informação.

• D.

  grandezas e medidas e números.

• E.

  tratamento da informação e grandezas e medidas.

A escolha de uma receita para o trabalho em sala de aula

• A.

  mostra que todas as receitas são idênticas, porque relacionam sempre os ingredientes que devem ser utilizados.

• B.

  parece trazer algumas dificuldades para grupos de alunos que talvez desconheçam os ingredientes selecionados.

• C.

  permite identificar diferentes tipos de textos, a partir da construção de seu significado por meio da leitura.

• D.

  facilita a leitura por todos os alunos, porque os ingredientes e sua quantidade aparecem em linhas diferentes.

• E.

  traz orientações a respeito de uma alimentação saudável, ao fazer com que os alunos escolham os ingredientes e sua quantidade.